
【题目】已知抛物线的解析式为y=﹣ ![]() x2+bx+5.
x2+bx+5.
(1)当自变量 x≥2时,函数值y 随 x的增大而减少,求b 的取值范围;
(2)如图,若抛物线的图象经过点A(2,5),与x 轴交于点C,抛物线的对称轴与x 轴交于B.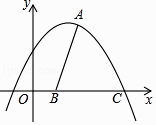
①求抛物线的解析式;
②在抛物线上是否存在点P,使得∠PAB=∠ABC?若存在,求出点P 的坐标;若不存在,请说明理由.
【答案】
(1)
解:抛物线的对称轴为:x=10b,
由题意可知:x≥2时,函数值y 随 x的增大而减少,
∴10b≤2,
∴b≤ ![]()
(2)
解:①将A(2,5)代入抛物线的解析式中,
∴5=﹣ ![]() ×4+2b+5,
×4+2b+5,
∴b= ![]() ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x+5,
x+5,
②由于∠PAB=∠ABC,
当P在对称轴的左侧时,
此时∠PAB=∠ABC,
∴PA∥BC,
∴P的纵坐标与A的纵坐标相同,
∴P(0,5),
当P在对称轴的右侧时,
连接AP并延长交x轴于E,
此时∠PAB=∠ABC
∴AE=BE,
过点A作AG⊥x轴于点G,过点P作PH⊥x轴于点H,过点E作EF⊥AB于点F,
∵B(1,0),A(2,5),
∴AG=5,BG=1,
∴由勾股定理可知:AB= ![]() ,
,
∵AE=BE,EF⊥AB,
∴BF= ![]() AB=
AB= ![]() ,
,
∵cos∠ABC= ![]() =
= ![]() ,
,
∴cos∠ABC= ![]() =
= ![]() ,
,
∴BE=13,
∴GE=BE﹣BG=12,
∴tan∠PEG= ![]() =
= ![]() ,
,
设P(x,﹣ ![]() x2+
x2+ ![]() x+5),
x+5),
∵E(14,0),
∴HE=14﹣x,PH=﹣ ![]() x2+
x2+ ![]() x+5,
x+5,
∴tan∠PEG= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得:x=2(舍去)或x= ![]() ,
,
∴P( ![]() ,
, ![]() )
)
综上所述,P(0,5)或P( ![]() ,
, ![]() )
)

【解析】(1)由题意可知:对称轴只需要小于或等于2即可,从而可求出b的范围;(2)①将A代入抛物线解析式即可求出b的值.②由于∠PAB=∠ABC,且P在抛物线上,故需要对P的位置进行分类讨论即可.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 . 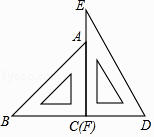
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF. 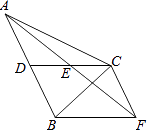
(1)求证:CF=AD;
(2)若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)当m>1时过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学八年级一班准备在“七一”组织参加红色旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去我市龙州县红八军纪念馆参加的学生数”的扇形圆心角为60°,则下列说法中正确的是( )
A.想去龙州县红八军纪念馆参加的学生占全班学生的60%
B.想去龙州县红八军纪念馆参观的学生有12人
C.想去龙州县红八军纪念馆参观的学生肯定最多
D.想去龙州县红八军纪念馆参观的学生占全班学生的 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F. 
(1)求证:AB=AC;
(2)若AD=2 ![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com