
����Ŀ��Ϊ�����Сѧ�������⣬��Ӫ�и��������꽫������������Сѧ��ij�ؼƻ���A��B����ѧУ���и�����������Ԥ�㣬������2��A��ѧУ��3��B��ѧУ�����ʽ�7800��Ԫ��������3��A��ѧУ��1��B��ѧУ�����ʽ�5400��Ԫ��
��1��������1��A��ѧУ��1��B��ѧУ�����ʽ�ֱ��Ƕ�����Ԫ��
��2�����ؼƻ�������A��B����ѧУ��10�����������ʽ��ɹ��Ҳ����͵ط�������ͬ�е��������Ҳ��������ʽ���11800��Ԫ���ط�����Ͷ���ʽ�����4000��Ԫ�����еط�����Ͷ�뵽A��B����ѧУ�ĸ������ʽ�ֱ�Ϊÿ��300��Ԫ��500��Ԫ�����ʹ����ļ��ָ�����������
���𰸡�
��1���⣺�������һ��A���һ��B��ѧУ�����ʽ�ֱ�Ϊx��Ԫ��y��Ԫ
������� ![]() �����
����� ![]() ��
��
�𣺸�����һ��A��ѧУ��һ��B��ѧУ�����ʽ�ֱ�Ϊ1200��Ԫ��1800��Ԫ��
��2���⣺����������A��ѧУa�����������B��ѧУ��10��a������
������ã� ![]() �����
����� ![]() ��
��
��3��a��5��
��xȡ������
��x=3��4��5��
������3�ַ�����
����һ��������A��ѧУ3����B��ѧУ7����
��������������A��ѧУ4����B��ѧУ6����
��������������A��ѧУ5����B��ѧУ5����
����������1���ɸ��ݡ�������2��A��ѧУ��3��B��ѧУ�����ʽ�7800��Ԫ��������3��A��ѧУ��1��B��ѧУ�����ʽ�5400��Ԫ�����г�����������𰸣���2��Ҫ���ݡ����Ҳ��������ʽ���11800��Ԫ���ط�����Ͷ���ʽ�����4000��Ԫ�����г�����ʽ�飬�жϳ���ͬ�ĸ��췽����
�����㾫����������Ĺؼ���������һԪһ�β���ʽ���Ӧ�õ����֪ʶ������1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�E��F�ֱ���AD��BC���е㣬CE��AF�ֱ�BD��G��H���㣮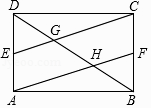
��֤��
��1���ı���AFCE��ƽ���ı��Σ�
��2��֤����EG=FH��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��ͼ1����O��ֱ��a��b�����У����ۡ�O���ת����ֱ��a��b֮��ľ���ʼ�ձ��ֲ��䣨���ڡ�O��ֱ���������ǰѾ�����һ���Ե�ͼ�γ�Ϊ���ȿ����ߡ���ͼ2������Բ����һ���Ե����ӣ�����ֱ����Բ�������������棬ͨ��Բ���������ý�С�����ȿ����ƶ�����ǰ������˵���Ű����˾������������ķ�������ʯ�Ƶ����������ģ� ��չӦ�ã���ͼ3��ʾ�Ļ������Σ�Ҳ��Ϊ���������Σ�Ҳ�ǡ��ȿ����ߡ�����ͼ4������ƽ����c��d֮�������������������ô������ƽ����ľ���ʼ�ղ��䣬��ֱ��c��d֮��ľ������2cm�������������ε��ܳ�Ϊcm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ൺ��ij��Ƶ������ʵ�е������������ּ۸��������ÿ��۸�ȵ������� ![]() ���±���ȥ��þƵ������ij�������ؼ�¼��
���±���ȥ��þƵ������ij�������ؼ�¼��
���� | ���� | |
δ��ס������ | 10 | 0 |
�������루Ԫ�� | 24000 | 40000 |
��1���þƵ�������ж��ټ䣿����ÿ��۸�Ϊ����Ԫ��
��2�������������٣�������ļ������䣮���г����鷢�֣�����������Ծ�ʵ��ȥ�������۸���ôÿ�춼����������۸�������ǣ���ôÿ����25Ԫ��ÿ��δ��ס����������1�䣮�������������أ��þƵ꽫������ļ۸����Ƕ���Ԫʱ�������������������ߣ�������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y= ![]() x��
x�� ![]() ��x�ύ�ڵ�B1 �� ��OB1Ϊ�߳����ȱ�������A1OB1 �� ����A1��A1B2ƽ����x�ᣬ��ֱ��l�ڵ�B2 �� ��A1B2Ϊ�߳����ȱ�������A2A1B2 �� ����A2��A2B3ƽ����x�ᣬ��ֱ��l�ڵ�B3 �� ��A2B3Ϊ�߳����ȱ�������A3A2B3 �� �������A2017�ĺ������� ��
��x�ύ�ڵ�B1 �� ��OB1Ϊ�߳����ȱ�������A1OB1 �� ����A1��A1B2ƽ����x�ᣬ��ֱ��l�ڵ�B2 �� ��A1B2Ϊ�߳����ȱ�������A2A1B2 �� ����A2��A2B3ƽ����x�ᣬ��ֱ��l�ڵ�B3 �� ��A2B3Ϊ�߳����ȱ�������A3A2B3 �� �������A2017�ĺ������� �� 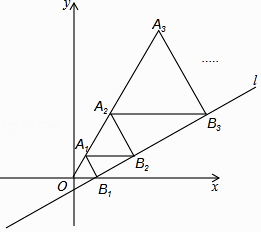
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�ضԽ���BD�۵���ʹ��A���ڵ�A'��������1=��2=50�㣬���A'Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017���ģ��ڱ߳�Ϊ2�ĵȱ�������ABC�У�P��BC��������һ�㣬���� P�ֱ��� PM��A B��PN��AC��M��N�ֱ�Ϊ���㣮 
��1����֤�����۵�P��BC�ߵĺδ�ʱ����PM+PN�ij�ǡ�õ���������ABCһ���ϵĸߣ�
��2����BP�ij�Ϊ��ֵʱ���ı���AMPN��������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĽ���ʽΪy=�� ![]() x2+bx+5��
x2+bx+5��
��1�����Ա��� x��2ʱ������ֵy �� x����������٣���b ��ȡֵ��Χ��
��2����ͼ���������ߵ�ͼ����A��2��5������x �ύ�ڵ�C�������ߵĶԳ�����x �ύ��B��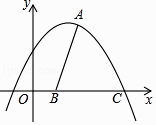
���������ߵĽ���ʽ��
�������������Ƿ���ڵ�P��ʹ�á�PAB=��ABC�������ڣ������P �����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+4��x�ύ��A����2��0����B��4��0�����㣬��y�ύ��C�㣮
��1���������ߵĽ���ʽ��
��2��T�������߶Գ����ϵ�һ�㣬�ҡ�ATC����ACΪ�ĵ��������Σ����T�����ꣻ
��3��M��Q����ֱ��A��B����ÿ��1����λ���ȵ��ٶ���x��ͬʱ����������У�����M��ԭ��ʱ����Q���̵�ͷ����ÿ�� ![]() ����λ���ȵ��ٶ����B�����ƶ�������M���������ߵĶԳ���ʱ������ֹͣ�˶�������M��ֱ��l��x�ύAC��BC�ڵ�P�����M���˶�ʱ��t���APQ���S�ĺ�����ϵʽ�������S�����ֵ��
����λ���ȵ��ٶ����B�����ƶ�������M���������ߵĶԳ���ʱ������ֹͣ�˶�������M��ֱ��l��x�ύAC��BC�ڵ�P�����M���˶�ʱ��t���APQ���S�ĺ�����ϵʽ�������S�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com