
����Ŀ����ͼ����֪������y=��![]() +bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
��1���������ߵĽ���ʽ����Գ��᷽�̣�
��2������AC��BC�����жϡ�AOC���COB�Ƿ����ƣ���˵�����ɣ�
��3��MΪ��������BC֮���һ�㣬NΪ�߶�BC�ϵ�һ�㣬��MN��y�ᣬ��MN�����ֵ��
��4���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
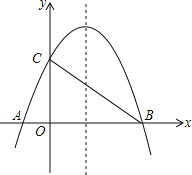
���𰸡���1��![]() ���Գ��
���Գ��![]() ��
��
��2�����ƣ����ɼ����������
��3��4��
��4��Q1��3��0����Q2��3��![]() ������Q3��3��
������Q3��3��![]() ����
����
��������
���⣨1���ѵ�B��������������߽���ʽ���b��ֵ�����ɵõ������߽���ʽ���ٸ��ݶԳ��᷽����ʽ���㼴�ɵý⣻
��2����y=0���ⷽ�������A�����꣬��x=0���y��ֵ�õ���C�����꣬�����OA��OB��OC��Ȼ����ݶ�Ӧ�߳ɱ������н���ȵ���������������֤����
��3����ֱ��BC�Ľ���ʽΪ![]() �����ô���ϵ�����������ʽ���ٱ�ʾ��MN��Ȼ����ݶ��κ�������ֵ������
�����ô���ϵ�����������ʽ���ٱ�ʾ��MN��Ȼ����ݶ��κ�������ֵ������
��4�����ù��ɶ�����ʽ���AC������C��CD���Գ�����D��Ȼ�����AC=CQʱ�����ù��ɶ�����ʽ���DQ���ֵ�Q�ڵ�D���Ϸ����·�������������Q��x��ľ��룬��д��������꼴�ɣ�����QΪ�Գ�����x��Ľ���ʱ��AQ=CQ����д����Q�����꼴�ɣ�
�����������1������B��8��0����������![]() �ϣ���
�ϣ���![]() �����
�����![]() ���������ߵĽ���ʽΪ
���������ߵĽ���ʽΪ![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��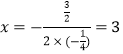 ��
��
��2����AOC�ס�COB���������£���y=0����![]() ����
����![]() �����
�����![]() ��
��![]() ������A����������2��0������x=0����y=4������C��������0��4������OA=2��OB=8��OC=4����
������A������Ϊ����2��0������x=0����y=4������C������Ϊ��0��4������OA=2��OB=8��OC=4����![]() =2����AOC=��COB=90�������AOC�ס�COB��
=2����AOC=��COB=90�������AOC�ס�COB��
��3����ֱ��BC�Ľ���ʽΪ![]() ����
����![]() ����ã�
����ã�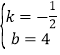 ����ֱ��BC�Ľ���ʽΪ
����ֱ��BC�Ľ���ʽΪ![]() ����MN��y�ᣬ��MN=
����MN��y�ᣬ��MN=![]() =
=![]() =
=![]() ������x=4ʱ��MN��ֵ������ֵΪ4��
������x=4ʱ��MN��ֵ������ֵΪ4��
��4���ɹ��ɶ����ã�AC=![]() ������C��CD���Գ�����D����CD=3����AC=CQʱ��DQ=
������C��CD���Գ�����D����CD=3����AC=CQʱ��DQ=![]() =
=![]() =
=![]() ��
��
��Q�ڵ�D���Ϸ�ʱ����Q��x��ľ���Ϊ![]() ����ʱ��Q1��3��
����ʱ��Q1��3��![]() ����
����
��Q�ڵ�D���·�ʱ����Q��x��ľ���Ϊ![]() ����ʱ��Q2��3��
����ʱ��Q2��3��![]() ����
����
����QΪ�Գ�����x��Ľ���ʱ��AQ=5��CQ=![]() =5����AQ=CQ����ʱ����Q3��3��0����
=5����AQ=CQ����ʱ����Q3��3��0����
������������Q��������3��![]() ����3��
����3��![]() ����3��0��ʱ����ACQΪ����������ʱ��
����3��0��ʱ����ACQΪ����������ʱ��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ���������С�������ᣬ����С������һ����������û���ã�ʹ����������������������ȥ������һ���һ������ѡ���
��1�����С����һ�ⲻʹ��������������ôС����Ե�һ����ĸ�����������
��2�����С���������������ڵڶ���ʹ�ã�������״ͼ�����б�������С��˳��ͨ�صĸ��ʣ�
��3���Ӹ��ʵĽǶȷ������㽨��С���ڵڼ���ʹ��������������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
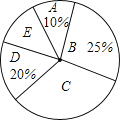
����Ŀ������������ѧ�������������ձ��½���ijУΪ����߱�Уѧ�����������ʣ���ʵ�������š���Уѧ��ÿ����������ʱ�䲻����1Сʱ�����ļ����Բ���ѧ����ÿ����������ʱ������˵���ͳ�ƣ������DZ��ε�������ͳ�Ʊ���ͳ��ͼ��
��� | A | B | C | D | E |
ʱ��t�����ӣ� | t��40 | 40��t��60 | 60��t��80 | 80��t��100 | t��100 |
���� | 12 | 30 | a | 24 | 12 |
��1��������α������ѧ������
��2�������ͳ�Ʊ���a��ֵ��
��3�������������������
��4�����ݵ�������������Ƹ�У2400��ѧ����ÿ����������ʱ�䲻����1Сʱ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪������y��x2��2ax+b�Ķ�����x���ϣ�P��x1��m����Q��x2��m����x1��x2���Ǵ��������ϵ����㣮
��1����a��1��
�ٵ�m��bʱ����x1��x2��ֵ��
�ڽ���������y��ƽ�ƣ�ʹ������x������������ľ���Ϊ4������������һ�仯���̣�
��2��������ʵ��c��ʹ��x1��c��1����x2��c+7��������m��ȡֵ��Χ��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=ax2+bx+c��������ֱ��ڵ�A��0��6����B��6��0����C����2��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������ߵĽ���ʽ��
��2������P�˶���ʲôλ��ʱ����PAB����������ֵ��
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵĺ�30��ǵ�ֱ�����ǰ��ص���һ����ͼ������A��B��C����AC���е�Mת����б��A��B��պù���ABC��ֱ�Ƕ���C��������ABC��б��AB���ڵ�N������AA�䡢C��C��AC�䣮��AC�ij�Ϊ2��������������ۣ���AA��=1����C��C��A��B�䣻����N�DZ�AB���е㣻���ı���AA��CC��Ϊ���Σ���A��N=B��C=![]() ��������ȷ���У�������
��������ȷ���У�������
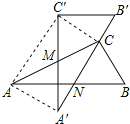
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��b��cΪ��������a��0����ͼ��x����A����2��0���͵�B����y�Ḻ�����ڵ�C�������߶Գ���Ϊx=��![]() �����н����У�����Ľ����ǣ�������
�����н����У�����Ľ����ǣ�������
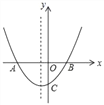
A. abc��0
B. ����ax2+bx+c=0�Ľ���x1=��2��x2=1
C. b2��4ac��0
D. a=b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��
��1��������AOBƽ�ƺ�������Σ���ƽ�ƺ�ķ���Ϊ����AD�ķ���ƽ�Ƶľ���ΪAD�ij���
��2���۲�ƽ�ƺ��ͼ�Σ����˾���ABCD�⣬����һ�������ƽ���ı��Σ���֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��,��ABC�����������ֱ�ΪA(2��2)��B(4,1��,C(4,4).��������������ÿ��С�����εı߳��� 1����λ���ȣ���
��1����������ABC�Ƶ�O ˳ʱ����ת90�ȵõ��ġ�A1B1C1��
��2��д��A1��B1��C1�����ꣻ
��3������߶�AC����ת��������ɨ����������������![]() ����
����
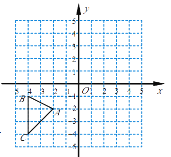
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com