
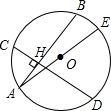
 如图,在⊙O中,弦AB⊥CD,H为垂足,AE是O的直径.求证:HA2+HD2+HC2+HB2=AE2.
如图,在⊙O中,弦AB⊥CD,H为垂足,AE是O的直径.求证:HA2+HD2+HC2+HB2=AE2. 分析 连接BO,DO,作OG⊥CD于点G,作OF⊥AB于点F”构造矩形OGHF,然后利用勾股定理和垂径定理,求得OG2+OF2=OH2,因为HA2+HD2+HC2+HB2=(HA+HB)2-2HA•HB+(HC+HD)2-2HC•HD=AB2+CD2-4HA•HB,过点H作直径MN,根据相交弦定理得出HA•HB=HM•HN=(R-OH)(R+OH)=R2-OH2,代入得到HA2+HD2+HC2+HB2=4R2=(2R)2=AE2.
解答  解:∵HA2+HD2+HC2+HB2=(HA+HB)2-2HA•HB+(HC+HD)2-2HC•HD=AB2+CD2-4HA•HB,
解:∵HA2+HD2+HC2+HB2=(HA+HB)2-2HA•HB+(HC+HD)2-2HC•HD=AB2+CD2-4HA•HB,
如图,过点H作直径MN,则HM•HN=HA•HB,
∴HA2+HD2+HC2+HB2=AB2+CD2-4HM•HN,
∵HM•HN=(R-OH)(R+OH)=R2-OH2
∴HA2+HD2+HC2+HB2=AB2+CD2-4(R2-OH2)=AB2+CD2-4R2+4OH2,
作OG⊥CD于点G,作OF⊥AB于点F,
∵DC⊥AB,OG⊥CD,OF⊥AB,
∴四边形OGHF为矩形;
∵FH2+OF2=OH2(勾股定理),
又∵FH2=OG2
∴OG2+OF2=OH2;
∵OF2=BO2-BF2=R2-$\frac{1}{4}$AB2;
又∵OG2=OD2-GD2=R2-$\frac{1}{4}$CD2,
∴HA2+HD2+HC2+HB2
=AB2+CD2-4R2+4(R2-$\frac{1}{4}$AB2+R2-$\frac{1}{4}$CD2)
=4R2
=(2R)2,
∵AE=2R,
∴HA2+HD2+HC2+HB2=AE2.
点评 本题主要考查了的是垂径定理和勾股定理.解得该题的关键是通过作辅助线构建矩形OFHG,利用勾股定理、矩形的性质以及垂径定理将 AB2+CD2联系在同一个等式中,然后根据代数知识求解.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
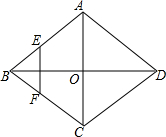 如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为4$\sqrt{7}$.
如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为4$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中.AD∥BC,过C作CE∥AB.P为梯形ABCD内一点,连结BP并延长交CD于F,交CE于E,再连结PC.若BP=PC.求证:△PFC∽△PCE.
如图,在等腰梯形ABCD中.AD∥BC,过C作CE∥AB.P为梯形ABCD内一点,连结BP并延长交CD于F,交CE于E,再连结PC.若BP=PC.求证:△PFC∽△PCE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com