
【题目】如图,△AOB中,A(-8,0),B(0, ![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
(1)⊙P的半径为 ;
(2)求证:EF为⊙P的切线;
(3)若点H是![]() 上一动点,连接OH、FH,当点H在
上一动点,连接OH、FH,当点H在![]() 上运动时,试探究
上运动时,试探究![]() 是否为定值?若为定值,求其值;若不是定值,请说明理由.
是否为定值?若为定值,求其值;若不是定值,请说明理由.

【答案】(1)5;(2)证明见解析;(3)![]() 是定值,
是定值, ![]()
【解析】试题分析:(1)根据勾股定理求得AB=![]() ,根据角平分线上的点到角两边的距离相等,得到AE=AO=8,BE=
,根据角平分线上的点到角两边的距离相等,得到AE=AO=8,BE=![]() ,在△BEC中,根据勾股定理求得CO=CE=4,再依据△AOC∽△COD求得OD=2,进而求得半径为5;(2)依据角平分线证得PC//AE,得到CP⊥EF;(3)根据△POH∽△PHF求得
,在△BEC中,根据勾股定理求得CO=CE=4,再依据△AOC∽△COD求得OD=2,进而求得半径为5;(2)依据角平分线证得PC//AE,得到CP⊥EF;(3)根据△POH∽△PHF求得![]() .
.
试题解析:
(1)5
(2)证明:连接CP,
∵AP=CP
∴∠PAC=∠PCA
∵AC平分∠OAB
∴∠PAC=∠EAC
∴∠PCA=∠EAC
∴PC//AE
∵CE⊥AB
∴CP⊥EF即EF是⊙P的切线
(3)![]() 是定值,
是定值, ![]()
连接PH,
由(1)得AP=PC=PH=5,∵A(-8,0) ∴OA=8 ∴OP=OA-AP=3
在Rt△POC中, ![]()
由射影定理可得![]() ,∴OF=
,∴OF=![]() , ∴PF=PO+OF=
, ∴PF=PO+OF=![]()
∵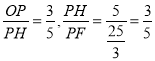 , ∴
, ∴![]() 又∵∠HPO=∠FPH
又∵∠HPO=∠FPH
∴△POH∽△PHF
∴![]() ,
,
当H与D重合时, ![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
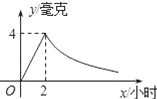
【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′//AB,ND′//BC,则∠D的度数为( )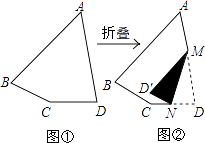
A.70°
B.75°
C.80°
D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
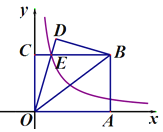
【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线![]() 经过点E,则k=_____;
经过点E,则k=_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“绿色出行”,减少雾霾,家住番禺在广州中心城区上班的王经理,上班出行由自驾车改为乘坐地铁出行,已知王经理家距上班地点21千米,他用地铁方式平均每小时出行的路程,比他用自驾车平均每小时行驶的路程的2倍还多5千米,他从家出发到达上班地点,地铁出行所用时间是自驾车方式所用时间的![]() . 求王经理地铁出行方式上班的平均速度.
. 求王经理地铁出行方式上班的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求![]() 的值;
的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子![]() 的值会发生变化吗?若不变,求出该值;若变化请说明理由.
的值会发生变化吗?若不变,求出该值;若变化请说明理由.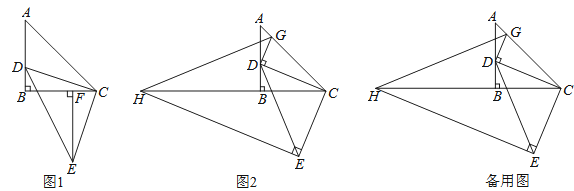
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
(1)求∠BDC的度数.
(2)求AC的长度.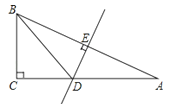
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com