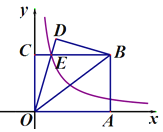
【题目】如图，在直角坐标系中，矩形OABC的顶点A在x轴上，顶点C在y轴上，B（4，3），连接OB，将△OAB沿直线OB翻折，得△ODB，OD与BC相交于点E，若双曲线经过点E，则k=_____；

参考答案：

【答案】

【解析】由翻折可知BD=OC, ∠D=∠BCO, 又∵∠CEO=∠DEB,

∴△COE∽△DBE.

∴OE=BE,

设CE=x，则OE=8-x，

在Rt△COE中，根据勾股定理得OC+CE=OE,即3+x=（4-x），解得，

∴k=.

点睛:折叠与翻折类试题主要有四个特点:(1)折叠与翻折类试题常常与线段垂直平分线，等腰三角形，全等三角形，相似三角形，解直角三角形等内容结合在一起；（2）在折叠与翻折的过程中寻找不变量，在折叠与翻折的过程中挖掘新生成的特殊图形（或常见的基本图形），立足翻折不变量，考查翻折的新生成；（3）将方程，锐角三角函数，解直角三角形和折叠与翻折融合在一起考查；（4）直角，中点，角平分线，相似三角形，锐角三角函数，解直角三角形，方程思想，转化与化归是解决折叠与翻折问题的常见关键词.

关闭