
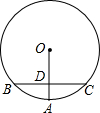
 如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.  新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:填空题
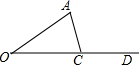 如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.
如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
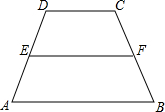 如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
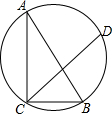 如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
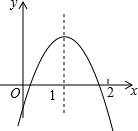 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
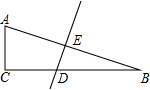 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
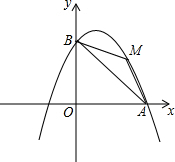 如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.
如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com