
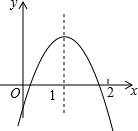 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论:分析 根据函数的图象,可以得到a<0,b>0,c<0,对称轴x=1,x=1时和x=-1时对应的函数值的正负,然后通过灵活变形得到题目中各结论所求的式子的结果,然后对照即可解答本题.
解答 解:由图象可得,
$-\frac{b}{2a}=1$,a<0,b>0,c<0,
∴b=-2a,a+c<0,-b<0,
∵x=1时,y=a+b+c>0;x=-1时,y=a-b+c<0,
∴a+c>-b,a-(-2a)+c<0,
∴|a+c|<|-b|,3a+c<0,故②正确,
∴(a+c)2<(-b)2,
即(a+c)2<b2,故①正确,
又∵x=1时,y=a+b+c>0,b=-2a,
∴a+b+c=$-\frac{b}{2}+b+c=\frac{b}{2}+c>0$,
∴b+2c>0,故③正确,
如果一元二次方程ax2+bx+c=-3有两个实根x1、x2,
则${x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{-2a}{a}=2$,故④错误,
故答案为:④.
点评 本题考查二次函数图象与系数的关系,解题的关键是明确二次函数图象的特点,运用数形结合的思想,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
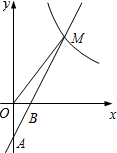 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
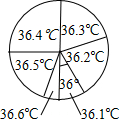 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )| 体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
| 人数(人) | 4 | 8 | 8 | 10 | x | 2 |
| A. | 这些体温的众数是8 | B. | 这些体温的中位数是36.35 | ||
| C. | 这个班有40名学生 | D. | x=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
如图,抛物线y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
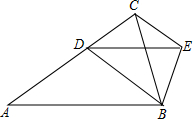 如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;
如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{b}{a}}$ | C. | $\sqrt{a+4}$ | D. | $\sqrt{50}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com