练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．方程$\sqrt{2x+3}$=2的解是$x=\frac{1}{2}$．

    分析 根据解无理方程的方法可以解答本题．

    解答 解：$\sqrt{2x+3}$=2，
    两边平方，得
    2x+3=4，
    解得x=$\frac{1}{2}$，
    检验：当x=$\frac{1}{2}$时，$\sqrt{2x+3}=\sqrt{2×\frac{1}{2}+3}=\sqrt{1+3}=\sqrt{4}=2$，
    故原无理方程的解是x=$\frac{1}{2}$．
    故答案为：x=$\frac{1}{2}$．

    点评 本题考查解无理方程，解题的关键是明确解无理方程的解，注意最后要进行检验．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．如图，由于各人的习惯不同，双手交叉时左手大拇指或右手大拇指在上是一个随机事件，曾老师对他任教的学生做了一个调查，统计结果如下表所示：
    2011届2012届2013届2014届2015届
    参与实验的人数10611098104112
    右手大拇指在上的人数5457495156
    频率0.5090.5180.5000.4900.500
    根据表格中的数据，你认为在这个随机事件中，右手大拇指在上的概率可以估计为（　　）
    A．0.6B．0.5C．0.45D．0.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

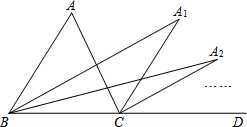    18．如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，…∠An-1BC的平行线与∠An-1CD的平分线交于点An，设∠A=θ，则∠An=$\frac{θ}{{2}^{n}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

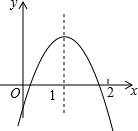    15．二次函数y=ax2+bx+c的图象如图所示，下列结论：
    ①（a+c）2＜b2；②3a+c＜0；③2c+b＞0；④如果一元二次方程ax2+bx+c=-3有两个实根x1、x2，那么x1+x2=1．
    其中结论错误的是④．（只填写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知AB、AC分别是同一个圆的内接正方形和内接正六边形的边，那么∠BAC的度数是15或105度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解方程：$\frac{x-4}{{{x^2}+2x}}+\frac{2}{{{x^2}-4}}=\frac{1}{{{x^2}-2x}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．为了了解某区5500名初三学生的体重情况，随机抽测了400名学生的体重，统计结果列表如下：
    体重（千克）频数频率
    40-4544
    45-5066
    50-5584
    55-6086
    60-6572
    65-7048
    那么样本中体重在50-55范围内的频率是0.21．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．（1）如图（1），分别以Rt△ABC三边为直径向外作三个正方形，其面积分别用S1，S2，S3表示，写出S1，S2，S3之间关系．（不必证明）
    （2）如图（2），分别以Rt△ABC三边为边向外作三个半圆，其面积分别用S1，S2，S3表示，确定它们的关系证明；
    （3）如图（3），分别以Rt△ABC三边为边向外作正三角形，其面积分别用S1，S2，S3表示，确定它们的关系并证明．

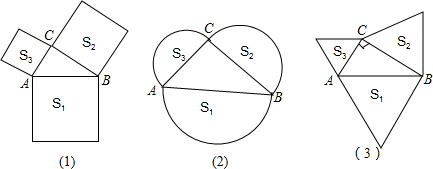
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，圆锥的底面半径为6cm，高为8cm，那么这个圆锥的母线l是10cm．

    查看答案和解析>>

    同步练习册答案