
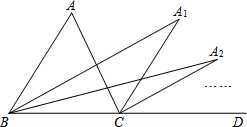
 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.
如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$. 分析 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,然后整理得到∠A1=$\frac{1}{2}$∠A,同理可得∠A2=$\frac{1}{2}$∠A1,从而判断出后一个角是前一个角的$\frac{1}{2}$,然后表示出,∠An即可.
解答 解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
∴∠A1+∠A1BC=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+∠A1BC,
∴∠A1=$\frac{1}{2}$∠A,
同理可得∠A2=$\frac{1}{2}$∠A1=$\frac{θ}{4}$=$\frac{θ}{{2}^{2}}$,
…,
∠An=$\frac{θ}{{2}^{n}}$.
故答案为:$\frac{θ}{{2}^{n}}$.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的$\frac{1}{2}$是解题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | -10m | B. | -5$\sqrt{2}$m | C. | 5$\sqrt{2}$m | D. | 10$\sqrt{2}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
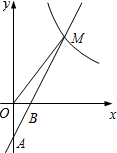 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
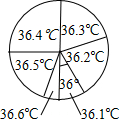 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )| 体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
| 人数(人) | 4 | 8 | 8 | 10 | x | 2 |
| A. | 这些体温的众数是8 | B. | 这些体温的中位数是36.35 | ||
| C. | 这个班有40名学生 | D. | x=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
如图,抛物线y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
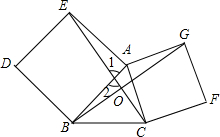 如图,已知锐角△ABC中,以AB,AC为边向外作正方形ABDE和正方形ACFG,连结CE、BG,交点为O,求证:(1)EC=BG;(2)EC⊥BG.
如图,已知锐角△ABC中,以AB,AC为边向外作正方形ABDE和正方形ACFG,连结CE、BG,交点为O,求证:(1)EC=BG;(2)EC⊥BG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com