
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n=400时,绿豆发芽的频率为0.955,所以绿豆发芽的概率是0.955;
②根据上表,估计绿豆发芽的概率是0.95;
③若n为4000,估计绿豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ① B. ①② C. ①③ D. ②③
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,边长为
中,边长为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ;同时点
;同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为
,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
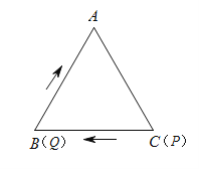
(1)当![]() 时,
时,![]() _______(用含
_______(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,求
时,求![]() 的值,并直接写出此时
的值,并直接写出此时![]() 为什么特殊的三角形?
为什么特殊的三角形?
(3)当![]() ,且
,且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数的图象经过(﹣1,﹣1),(0,0),(1,9)三点
(1)求这个二次函数的解析式.
(2)若另外三点(x1,21),(x2,21),(x1+x2,n)也在该二次函数图象上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .将等腰直角形
.将等腰直角形![]() 沿高
沿高![]() 剪开后,拼成图2所示的正方形
剪开后,拼成图2所示的正方形![]() .
.
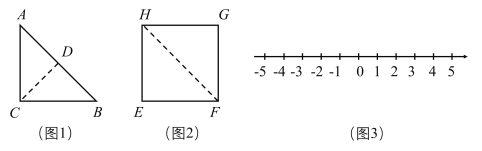
(1)如图1,等腰直角三角形![]() 的面积是______________.
的面积是______________.
(2)如图2,求正方形![]() 的边长是多少?
的边长是多少?
(3)把正方形![]() 放到数轴上(如图3),使得边
放到数轴上(如图3),使得边![]() 落到数轴上,其中一个端点所对应的数为-1,直接写出另一个端点所对应的数.
落到数轴上,其中一个端点所对应的数为-1,直接写出另一个端点所对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上以
上以![]() 的速度由
的速度由![]() 向终点
向终点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向终点
向终点![]() 运动,它们运动的时间为
运动,它们运动的时间为![]() .
.
(解决问题)
若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,回答下面的问题:
时,回答下面的问题:
(1)![]() ;
;
(2)此时![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;

(3)求证:![]() ;
;
(变式探究)
若点![]() 的运动速度为
的运动速度为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 全等?若存在,请直接写出相应的
全等?若存在,请直接写出相应的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() ,宽为
,宽为![]() 的全等小矩形,且
的全等小矩形,且![]() .
.
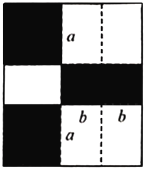
(1)观察图形,将多项式![]() 分解因式;
分解因式;
(2)若每块小矩形的面积为10,四个正方形的面积和为58.求下列代数式的值:
①![]() .
.
②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C为线段OB的中点,D为线段OA上一点.连结AC、BD交于点P.
(问题引入)(1)如图1,若点P为AC的中点,求![]() 的值.
的值.
温馨提示:过点C作CE∥AO交BD于点E.
(探索研究)(2)如图2,点D为OA上的任意一点(不与点A、O重合),求证:![]() .
.
(问题解决)(3)如图2,若AO=BO,AO⊥BO,![]() ,求tan∠BPC的值.
,求tan∠BPC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() 轴,且经过(0,0),(
轴,且经过(0,0),(![]() )两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
)两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
(1)求![]() 的值;
的值;
(2)求证:点P在运动过程中,⊙P始终与![]() 轴相交;
轴相交;
(3)设⊙P与![]() 轴相交于M
轴相交于M![]() ,N
,N ![]() (
(![]() <
<![]() )两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
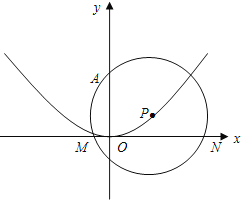
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com