
(本题满分10分)
如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形AB-CD的边AB上的“强相似点”,解决问题:
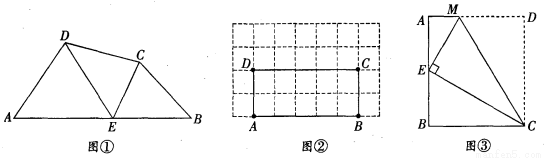
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由:
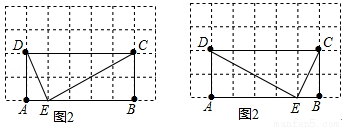
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
(1)是;(2)作图见试题解析;(3)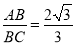 .
.
【解析】
试题分析:(1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解;
(2)以CD为直径画弧,取该弧与AB的一个交点即为所求;
(3)由点E是矩形ABCD的AB边上的一个强相似点,得△AEM∽△BCE∽△ECM,根据相似三角形的对应角相等,可求得∠BCE=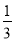 ∠BCD=30°,利用含30°角的直角三角形性质可得BE与AB,BC边之间的数量关系,从而可求出AB与BC边之间的数量关系.
∠BCD=30°,利用含30°角的直角三角形性质可得BE与AB,BC边之间的数量关系,从而可求出AB与BC边之间的数量关系.
试题解析:(1)∵∠A=∠B=∠DEC=45°,∴∠AED+∠ADE=135°,∠AED+∠CEB=135°,∴∠ADE=∠CEB,
在△ADE和△BEC中,∵∠A=∠B,∠ADE=∠BEC,∴△ADE∽△BEC,∴点E是四边形ABCD的边AB上的相似点;
(2)如图所示:点E是四边形ABCD的边AB上的强相似点,
(3)∵点E是四边形ABCM的边AB上的一个强相似点,∴△AEM∽△BCE∽△ECM,∴∠BCE=∠ECM=∠AEM.由折叠可知:△ECM≌△DCM,∴∠ECM=∠DCM,CE=CD,∴∠BCE=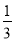 ∠BCD=30°,BE=
∠BCD=30°,BE=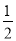 CE=
CE=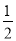 AB,在Rt△BCE中,tan∠BCE=
AB,在Rt△BCE中,tan∠BCE=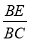 =tan30°=
=tan30°=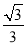 ,∴
,∴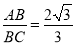 .
.
考点:相似形综合题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:2014-2015学年福建省南平市水东学校七年级上学期期中考试数学试卷(解析版) 题型:解答题
在数轴上表示下列各数,并按从小到大的顺序用“<”号连接起来.
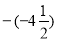 , +3 , 0 ,
, +3 , 0 , 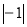 , -
, -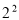 ,
, 

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级12月学情监测数学试卷(解析版) 题型:选择题
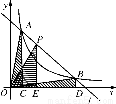
如图261,直线l和双曲线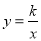 (
(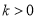 )交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是
)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是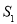 ,△BOD面积是
,△BOD面积是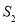 ,△POE面积是
,△POE面积是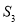 ,则( )
,则( )
A.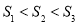 B.
B.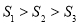 C.
C. D.
D.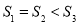
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级12月学情监测数学试卷(解析版) 题型:选择题
如图小正方形的边长均为l,则下列图中的三角形(阴影部分)与△ABC相似的是( )
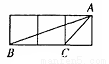
A. B.
B.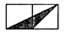 C.
C. D.
D.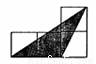
查看答案和解析>>
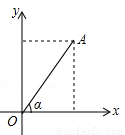
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=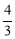 ,则t的值为 .
,则t的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com