
【题目】为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩只分A、B、C、D四个阶段.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表: 根据表中的信息,解决下列问题:
成绩等级 | A | B | C | D |
人数 | 60 | x | y | 10 |
占抽查学生总数的百分比 | 30% | 50% | 15% | m |
(1)本次抽查的学生共有名;
(2)表中x、y和m所表示的数分别为:X= , y= , m=;
(3)请补全条形统计图. 
【答案】
(1)200
(2)100;30;5%
(3)解:统计图为:
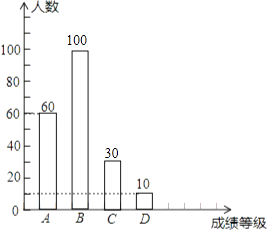
【解析】解:(1)观察统计图和统计表知道A组有60人,占总数的30%, 故抽查的总人数为:60÷30%=200人;(2)x=200×50%=100人,
y=200×15%=30人,
m=10÷200×100%=5%;
【考点精析】认真审题,首先需要了解统计表(制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD,BC于点E,F,作BH⊥AF于点H,分别交AC,CD于点G,P,连接GE,GF.
(1)求证:△OAE≌△OBG;
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由;
(3)试求: ![]() 的值(结果保留根号).
的值(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2? |
我的结果也正确!
(1)小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?
(2)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样…
(3)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由. 

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程![]() ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与![]() 对应的点,分别记作A,B;
对应的点,分别记作A,B;
(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上有两条直线AB、CD相交于点O,且∠BOD=150°(如图),现按如下要求规定此平面上点的“距离坐标”: ①点O的“距离坐标”为(0,0);
②在直线CD上,且到直线AB的距离为p(p>0)的点的“距离坐标”为(p,0);在直线AB上,且到直线CD的距离为q(q>0)的点的“距离坐标”为(0,q);
③到直线AB、CD的距离分别为p,q(p>0,q>0)的点的“距离坐标”为(p,q).
设M为此平面上的点,其“距离坐标”为(m,n),根据上述对点的“距离坐标”的规定,解决下列问题:
(1)画出图形(保留画图痕迹): ①满足m=1,且n=0的点M的集合;
②满足m=n的点M的集合;
(2)若点M在过点O且与直线CD垂直的直线l上,求m与n所满足的关系式.(说明:图中OI长为一个单位长) 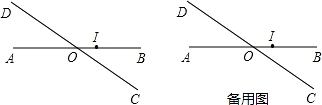
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有学生2100人,在“文明我先行”活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了100名学生,并制成统计表:校本课程意向统计表
课程类型 | 频数 | 频率(%) |
法律 | s | 0.08 |
礼仪 | a | 0.20 |
环保 | 27 | 0.27 |
感恩 | b | m |
互助 | 15 | 0.15 |
合计 | 100 | 1.00 |
请根据统计表的信息,解答下列问题;
(1)在这次调查活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);
(2)a= , b= , m=;
(3)如果要画“校本课程报名意向扇形统计图”,那么“礼仪”类校本课程对应的扇形圆心角的度数是;
(4)请你估计,选择“感恩”类校本课程的学生约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图. 
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com