Question

10．如图，D是AB中点，且CB=CD，E为△ABC外一点，满足CE=CA，过点B作BF⊥BC交EA延长线于E．求证：∠FDA=∠BEA．

Answer 1

分析 先判断出BDM是直角三角形，再利用等腰三角形“三线合一的性质”得出AH=EH，进而用三角形的中位线平行于第三边DH∥BE，继续判断出A、D、G、H四点在同一个圆上，再得出△ABF∽GMC，抓划出$\frac{BD}{GM}=\frac{BF}{BM}$，进而得出△BDF∽△MGB，再得出FN⊥BG，最后用同角的余角即可转化出结论．

解答 证明：如图，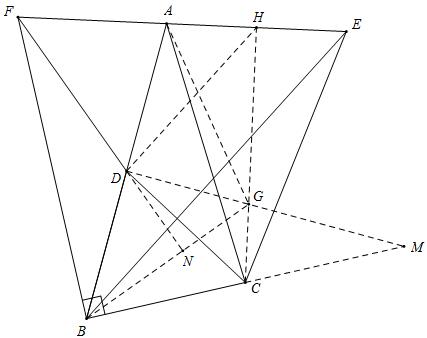

延长BC至点M，使CM=CB，连接MD，过点C作CH⊥AE于点H，交MD于点G，连接AG、BG、DH，延长FD交BG于点N，
∵CB=CD，
∴CM=CB=CD，
∴△BDM是直角三角形，且∠BDM=90°，
即MD⊥AD，
又∵D是AD的中点，
∴AG=BG（线段垂直平分线的性质），AD=BD，
∴∠AGD=∠BGD（等腰三角形“三线合一的性质”）；
∵CE=CA，CH⊥AE，
∴AH=EH（等腰三角形“三线合一的性质”），
又∵AD=BD，
∴DH∥BE（三角形的中位线平行于第三边），
∴∠BEA=∠DHA；
∵MD⊥AB，CH⊥AE，
∴∠ADG=∠AHG=90°，
∴∠ADG+∠AHG=180°，
∴A、D、G、H四点在同一个圆上，
∴∠AGD=∠DHA（同弧所对的圆周角相等），
∠BAF=∠DGH（圆内接四边形的一个外角等于它的内对角），
∴∠BEA=∠BGD；
∵BF⊥BC，∠BDM=90°，
∴∠FBM=∠BDM=90°，
∴∠ADF+∠MBD=90°，∠M+∠MBD=90°，
∴∠ABF=∠M（同角的余角相等），
∵∠BAF=∠DGH，∠MGC=∠DGH，
∴∠BAF=∠MGC，
∴△ABF∽GMC（有两个角对应相等的两个三角形相似），
∴$\frac{AB}{GM}=\frac{BF}{MC}$，
又∵AB=2BD，MC=$\frac{1}{2}$BM，
∴$\frac{2BD}{GM}=\frac{BF}{\frac{1}{2}BM}$，
即 $\frac{BD}{GM}=\frac{BF}{BM}$，
∵∠ABF=∠M，
∴△BDF∽△MGB（两边对应成比例且夹角相等的两个三角形相似），
∴∠BFD=∠MBG，
∴∠BFD+∠FBG=∠MBG+∠FBG，
即∠BFD+∠FBG=∠FBC=90°，
∴FN⊥BG，
∴∠BGD+∠GDN=90°，
∵∠ADG=90°，
∴∠FDA+∠GDN=90°，
∴∠BGD=∠FDA（同角的余角相等），
又∵∠BEA=∠BGD（已证），
∴∠FDA=∠BEA．

点评 此题是四点共圆，主要考查了直角三角形的判定和性质，相似三角形的性质和判定，等腰三角形的判定和性质等知识，解本题的关键是判断出A、D、G、H四点共圆，作出辅助线是解本题的难点，是一道比较好的竞赛题．