
分析 (1)方案一:总费用=贺卡的单价×贺卡的数量.方案二:费用=每张贺卡制作的成本×贺卡的数量+广告公司精制费.据此可得出方案一和方案二的函数关系式;
(2)本题只需让(1)中得出的两个函数关系式相等,求出x的值,就是所求的贺卡的张数;
(3)可将50张分别代入(1)中的两个函数式中,得出函数的值,然后比较哪种方案更便宜.
解答 解:(1)y1=8x,y2=4x+120;
(2)依题意y1=y2,
即8x=4x+120,
解得x=30,
故购买贺卡30张时,两种方案的费用相同;
(3)把x=50分别代入y1=8x,y2=4x+120中,
得y1=8×50=400,y2=4×50+120=320,
∵y1>y2,
∴需要贺卡50张时,采用方案二较便宜.
点评 本题考查了一次函数的应用,读清题意,找对等量关系是解题的关键,另外解决实际问题时还应有一定的生活经验.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
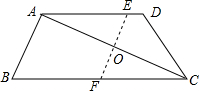 如图,在四边形ABCD中,AD∥BC,把四边形对折,使点A、C重合,折痕EF分别交AD于点E,交BC于点F.
如图,在四边形ABCD中,AD∥BC,把四边形对折,使点A、C重合,折痕EF分别交AD于点E,交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,AD=9,如果$\frac{BE}{BC}$=$\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$,BE=6.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,AD=9,如果$\frac{BE}{BC}$=$\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$,BE=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com