
分析 (1)根据立方差公式进行计算;
(2)先把(x2-xy+y2)2分组为[(x2+y2)-xy]2,再计算;
(3)先提公因式a+b,再根据乘法法则进行计算;
(4)直接根据多项式乘以多项式法则进行计算.
解答 解:(1)(4+m)(16-4m+m2),
=43+m3,
=64+m3;
(2)(x2+2xy+y2)•(x2-xy+y2)2;
=(x2+2xy+y2)•[(x2+y2)-xy]2,
=(x2+2xy+y2)•[(x2+y2)2-2xy(x2+y2)+x2y2],
=(x2+2xy+y2)(x2+y2)2-(x2+2xy+y2)•2xy(x2+y2)+x2y2(x2+2xy+y2),
=(x2+y2)(x2-y2)2+x2y2(x2+2xy+y2),
=(x2+2xy+y2)(x2+y2)(x2-2xy+y2)+x2y2(x2+2xy+y2),
=(x4-y4)(x2-y2)+x2y2(x2+2xy+y2),
=x6-x2y4-x4y2+y6+x4y2+2x3y3+x2y4;
(3)(a+b)(a2-ab+b2)-(a+b)3;
=(a+b)(a2-ab+b2-a2-2ab-b2),
=-3ab(a+b),
=-3a2b-3ab2;
(4)(a-4ab)($\frac{1}{4}$a2+4b2+ab),
=$\frac{1}{4}{a}^{3}$-a3b+4ab2-16ab3+a2b-4a2b2.
点评 本题整式的计算,熟练掌握多项式乘以多项式的法则是关键,多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.运用法则时应注意以下两点:①相乘时,按一定的顺序进行,必须做到不重不漏;②多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.


科目:初中数学 来源: 题型:填空题
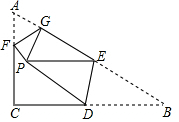 如图所示,在Rt△ABC纸片中,∠C=90°,∠B=30°,AC=6,将∠A、∠B向内翻折,使顶点A、B重合于一点P,折痕分别为FG和DE,若PE∥BC,BD=4,则PF=10-4$\sqrt{3}$.
如图所示,在Rt△ABC纸片中,∠C=90°,∠B=30°,AC=6,将∠A、∠B向内翻折,使顶点A、B重合于一点P,折痕分别为FG和DE,若PE∥BC,BD=4,则PF=10-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15.5cm | B. | 6.2cm | C. | 3.1cm | D. | 2.6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(-1,2) | B. | y随x的增大而增大 | ||
| C. | 图象关于原点对称 | D. | 若x>1,则y>-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
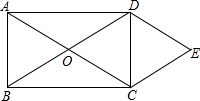 如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com