
ΓΨΧβΡΩΓΩΡ≥≥§ –Ρβ”Ύ÷–«οΫΎ«Α![]() Χλάοœζ έΡ≥ΤΖ≈Τ‘¬±ΐΘ§ΤδΫχΦέΈΣ
Χλάοœζ έΡ≥ΤΖ≈Τ‘¬±ΐΘ§ΤδΫχΦέΈΣ![]() ‘Σ/
‘Σ/![]() Θ°…ηΒΎ
Θ°…ηΒΎ![]() ΧλΒΡœζ έΦέΗώΈΣ
ΧλΒΡœζ έΦέΗώΈΣ![]() Θ®‘Σ/
Θ®‘Σ/![]() Θ©Θ§œζ έΝΩΈΣ
Θ©Θ§œζ έΝΩΈΣ![]() Θ°ΗΟ≥§ –ΗυΨί“‘ΆυΒΡœζ έΨ≠―ιΒΟ≥ω“‘œ¬ΒΡœζ έΙφ¬…ΘΚΔΌΒ±
Θ°ΗΟ≥§ –ΗυΨί“‘ΆυΒΡœζ έΨ≠―ιΒΟ≥ω“‘œ¬ΒΡœζ έΙφ¬…ΘΚΔΌΒ±![]() ±Θ§
±Θ§![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§
±Θ§![]() ”κ
”κ![]() ¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§«“Β±
¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§«“Β±![]() ±Θ§
±Θ§![]() ΘΜ
ΘΜ![]() ±Θ§
±Θ§![]() Θ°ΔΎ
Θ°ΔΎ![]() ”κ
”κ![]() ΒΡΙΊœΒΈΣ
ΒΡΙΊœΒΈΣ![]() Θ°
Θ°
Θ®1Θ©Β±![]() ±Θ§
±Θ§![]() ”κ
”κ![]() ΒΡΙΊœΒ ΫΈΣΓΓ ΓΓΘΜ
ΒΡΙΊœΒ ΫΈΣΓΓ ΓΓΘΜ
Θ®2Θ©![]() ΈΣΕύ…Ό ±Θ§Β±ΧλΒΡœζ έάϊ»σ
ΈΣΕύ…Ό ±Θ§Β±ΧλΒΡœζ έάϊ»σ![]() Θ®‘ΣΘ©Ήν¥σΘΩΉν¥σάϊ»σΈΣΕύ…ΌΘΩ
Θ®‘ΣΘ©Ήν¥σΘΩΉν¥σάϊ»σΈΣΕύ…ΌΘΩ
Θ®3Θ©»τ≥§ –œΘΆϊΒΎ![]() ΧλΒΫΒΎ
ΧλΒΫΒΎ![]() ΧλΒΡ»’œζ έάϊ»σ
ΧλΒΡ»’œζ έάϊ»σ![]() Θ®‘ΣΘ©Υφ
Θ®‘ΣΘ©Υφ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρ–η“Σ‘ΎΒ±Χλœζ έΦέΗώΒΡΜυ¥Γ…œ’«
ΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρ–η“Σ‘ΎΒ±Χλœζ έΦέΗώΒΡΜυ¥Γ…œ’«![]() ‘Σ/
‘Σ/![]() Θ§«σ
Θ§«σ![]() ΒΡΉν–Γ÷ΒΘ°
ΒΡΉν–Γ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΈΣ
ΈΣ![]() ±Θ§Β±ΧλΒΡœζ έάϊ»σ
±Θ§Β±ΧλΒΡœζ έάϊ»σ![]() Θ®‘ΣΘ©Ήν¥σΘ§Ήν¥σάϊ»σΈΣ
Θ®‘ΣΘ©Ήν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘ΣΘΜΘ®3Θ©3
‘ΣΘΜΘ®3Θ©3
ΓΨΫβΈωΓΩ
Θ®1Θ©“άΨίΧβ“βάϊ”Ο¥ΐΕ®œΒ ΐΖ®Θ§“ΉΒΟ≥ωΒ±![]() ±Θ§
±Θ§![]() ”κ
”κ![]() ΒΡΙΊœΒ ΫΈΣΘΚ
ΒΡΙΊœΒ ΫΈΣΘΚ![]() Θ§
Θ§
Θ®2Θ©ΗυΨίœζ έάϊ»σΘΫœζ έΝΩΓΝΘ® έΦέ©¹ΫχΦέΘ©Θ§Ν–≥ωΟΩΧλΒΡœζ έάϊ»σ![]() Θ®‘ΣΘ©”κœζ έΦέ
Θ®‘ΣΘ©”κœζ έΦέ![]() Θ®‘Σ/œδΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§‘Ό“άΨίΚ· ΐΒΡ‘ωΦθ–‘«σΒΟΉν¥σάϊ»σΘ°
Θ®‘Σ/œδΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§‘Ό“άΨίΚ· ΐΒΡ‘ωΦθ–‘«σΒΟΉν¥σάϊ»σΘ°
Θ®3Θ©“Σ ΙΒΎ![]() ΧλΒΫΒΎ
ΧλΒΫΒΎ![]() ΧλΒΡ»’œζ έάϊ»σ
ΧλΒΡ»’œζ έάϊ»σ![]() Θ®‘ΣΘ©Υφ
Θ®‘ΣΘ©Υφ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρΕ‘≥Τ÷α
ΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρΕ‘≥Τ÷α![]() Θ§«σΒΟ
Θ§«σΒΟ![]() Φ¥Ω…
Φ¥Ω…
Θ®1Θ©“άΧβ“βΘ§Β±![]() ±Θ§
±Θ§![]() ±Θ§
±Θ§![]() Θ§
Θ§
Β±![]() ±Θ§…η
±Θ§…η![]() Θ§
Θ§
‘ρ”–![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ
![]() ”κ
”κ![]() ΒΡΙΊœΒ ΫΈΣΘΚ
ΒΡΙΊœΒ ΫΈΣΘΚ![]()
Θ®2Θ©“άΧβ“βΘ§
![]()

’ϊάμΒΟΘ§ 
Β±![]() ±Θ§
±Θ§
![]() Υφ
Υφ![]() ‘ω¥σΕχ‘ω¥σ
‘ω¥σΕχ‘ω¥σ
![]() ±Θ§»ΓΉν¥σ÷Β
±Θ§»ΓΉν¥σ÷Β![]()
Β±![]() ±Θ§
±Θ§
![]()
![]()
![]() ±Θ§
±Θ§![]() »ΓΒΟΉν¥σ÷ΒΘ§¥Υ ±
»ΓΒΟΉν¥σ÷ΒΘ§¥Υ ±![]()
Ήέ…œΥυ ωΘ§![]() ΈΣ
ΈΣ![]() ±Θ§Β±ΧλΒΡœζ έάϊ»σ
±Θ§Β±ΧλΒΡœζ έάϊ»σ![]() Θ®‘ΣΘ©Ήν¥σΘ§Ήν¥σάϊ»σΈΣ
Θ®‘ΣΘ©Ήν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘Σ
‘Σ
Θ®3Θ©“άΧβ“βΘ§
![]()
![]()
![]() ΒΎ
ΒΎ![]() ΧλΒΫΒΎ
ΧλΒΫΒΎ![]() ΧλΒΡ»’œζ έάϊ»σ
ΧλΒΡ»’œζ έάϊ»σ![]() Θ®‘ΣΘ©Υφ
Θ®‘ΣΘ©Υφ![]() ΒΡ‘ω¥σΕχ‘ω¥σ
ΒΡ‘ω¥σΕχ‘ω¥σ
![]() Ε‘≥Τ÷α
Ε‘≥Τ÷α Θ§ΒΟ
Θ§ΒΟ![]()
Ι ![]() ΒΡΉν–Γ÷ΒΈΣ
ΒΡΉν–Γ÷ΒΈΣ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§»γΆΦ1Θ§≈ΉΈοœΏyΘΫax2+bx+cΒΡΕ‘≥Τ÷αΈΣ![]() Θ§”κx÷αΒΡΫΜΒψAΘ®©¹1Θ§0Θ©”κy÷αΫΜ”ΎΒψCΘ®0Θ§©¹2Θ©Θ°
Θ§”κx÷αΒΡΫΜΒψAΘ®©¹1Θ§0Θ©”κy÷αΫΜ”ΎΒψCΘ®0Θ§©¹2Θ©Θ°
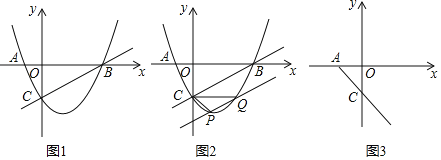
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ2Θ°ΒψP «÷±œΏBCœ¬ΖΫ≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§ΙΐΒψPΉςBCΒΡΤΫ––œΏΫΜ≈ΉΈοœΏ”ΎΒψQΘ®ΒψQ‘ΎΒψP”“≤ύΘ©Θ§Ν§ΫαBQΘ§Β±ΓςPCQΒΡΟφΜΐΈΣΓςBCQΟφΜΐΒΡ“ΜΑκ ±Θ§«σPΒψΒΡΉχ±ξΘΜ
Θ®3Θ©œ÷ΫΪΗΟ≈ΉΈοœΏ―Ί…δœΏACΒΡΖΫœρΫχ––ΤΫ“ΤΘ§ΤΫ“ΤΚσΒΡ≈ΉΈοœΏ”κ÷±œΏACΒΡΫΜΒψΈΣA'ΓΔC'Θ®ΒψC'‘ΎΒψA'ΒΡœ¬ΖΫΘ©Θ§”κx÷αΒΡΫΜΒψΈΣB'Θ§Β±ΓςAB'C'”κΓςAA'B'œύΥΤ ±Θ§«σ≥ωΒψAΓδΒΡΚαΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –Ρ≥÷–―ßΉι÷·≤ΩΖ÷―ß…ζ»ΞΡ≥ΒΊΩΣ’Ι―–―ß¬Ο––ΜνΕ·Θ§‘Ύ≤ΈΦ”¥Υ¥ΈΜνΕ·ΒΡ Π…ζ÷–Θ§»τΟΩΈΜάœ Π¥χ17Ηω―ß…ζΘ§ΜΙ Θ12Ηω―ß…ζΟΜ»Υ¥χΘΜ»τΟΩΈΜάœ Π¥χ18Ηω―ß…ζΘ§ΨΆ”–“ΜΈΜάœ Π…Ό¥χ4Ηω―ß…ζΘ§œ÷”–ΦΉΓΔ““ΝΫ÷÷¥σΩΆ≥ΒΘ§ΥϋΟ«ΒΡ‘ΊΩΆΝΩΚΆΉβΫπ»γ±μΥυ ΨΘ°
ΦΉ÷÷ΩΆ≥Β | ““÷÷ΩΆ≥Β | |
‘ΊΩΆΝΩ/Θ®»Υ/ΝΨΘ© | 30 | 42 |
ΉβΫπ/Θ®‘Σ/ΝΨΘ© | 300 | 400 |
―ß–ΘΦΤΜ°¥Υ¥Έ―–―ß¬Ο––ΜνΕ·ΒΡΉβ≥ΒΉήΖ―”Ο≤Μ≥§Ιΐ3100‘ΣΘ§ΈΣΝΥΑ≤»ΪΘ§ΟΩΝΨΩΆ≥Β…œ÷Ν…Ό“Σ”–2Οϊάœ ΠΘ°
Θ®1Θ©≤ΈΦ”¥Υ¥Έ―–―ß¬Ο––ΜνΕ·ΒΡάœ ΠΚΆ―ß…ζΗς”–Εύ…Ό»ΥΘΩ
Θ®2Θ©ΔΌΦ»“Σ±Θ÷ΛΥυ”– Π…ζΕΦ”–≥ΒΉχΘ§”÷“Σ±Θ÷ΛΟΩΝΨΩΆ≥Β…œ÷Ν…Ό“Σ”–2Οϊάœ ΠΘ§–ηΉβ”ΟΦΗΝΨΩΆ≥ΒΘΜ
ΔΎ«σΉβ≥ΒΖ―”ΟΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§AB=4Θ§AD=2Θ§ΒψE‘ΎCD…œΘ§DE=1Θ§ΒψF «±ΏAB…œ“ΜΕ·ΒψΘ§“‘EFΈΣ–±±ΏΉςRtΓςEFPΘ°»τΒψP‘ΎΨΊ–ΈABCDΒΡ±Ώ…œΘ§«“’β―υΒΡ÷±Ϋ«»ΐΫ«–Έ«ΓΚΟ”–ΝΫΗωΘ§‘ρAFΒΡ÷Β «________.
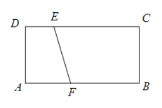
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Βψ![]() «œΏΕΈ
«œΏΕΈ![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() Θ§“‘Βψ
Θ§“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§![]() ΒΡ≥ΛΈΣΑκΨΕΉςΓ―
ΒΡ≥ΛΈΣΑκΨΕΉςΓ―![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΒΡ¥ΙœΏΫΜΓ―
ΒΡ¥ΙœΏΫΜΓ―![]() ”Ύ
”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§Βψ
ΝΫΒψΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ―”≥ΛœΏ…œΘ§Ν§Ϋ”
ΒΡ―”≥ΛœΏ…œΘ§Ν§Ϋ”![]() ΫΜΓ―
ΫΜΓ―![]() ”ΎΒψ
”ΎΒψ![]() Θ§“‘
Θ§“‘![]() Θ§
Θ§![]() ΈΣ±ΏΉς
ΈΣ±ΏΉς![]() Θ°
Θ°
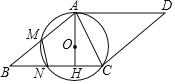
Θ®1Θ©«σ÷ΛΘΚ![]() «Γ―
«Γ―![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®2Θ©»τ![]() Θ§«σΥΡ±Ώ–Έ
Θ§«σΥΡ±Ώ–Έ![]() ”κΓ―
”κΓ―![]() ÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΘΜ
÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΘΜ
Θ®3Θ©»τ![]() Θ§
Θ§![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§«σ
Θ§«σ![]() ΚΆ
ΚΆ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΔΌΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“―÷Σ
÷–Θ§“―÷Σ![]() Θ§
Θ§![]() ΥΡΒψΘ§Ε·Βψ
ΥΡΒψΘ§Ε·Βψ![]() “‘ΟΩΟκ
“‘ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί![]() ‘ΥΕ·Θ®
‘ΥΕ·Θ®![]() ≤Μ”κΒψ
≤Μ”κΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ÷ΊΚœΘ©Θ§…η‘ΥΕ· ±ΦδΈΣ
÷ΊΚœΘ©Θ§…η‘ΥΕ· ±ΦδΈΣ![]() Θ®ΟκΘ©Θ°
Θ®ΟκΘ©Θ°
Θ®1Θ©«σΨ≠Ιΐ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΒψΒΡ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
»ΐΒψΒΡ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Βψ![]() ‘ΎΘ®
‘ΎΘ®![]() Θ©÷–ΒΡ≈ΉΈοœΏ…œΘ§Β±
Θ©÷–ΒΡ≈ΉΈοœΏ…œΘ§Β±![]()
![]() ΈΣ
ΈΣ![]() ΒΡ÷–Βψ ±Θ§»τ
ΒΡ÷–Βψ ±Θ§»τ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®3Θ©Β±![]() ‘Ύ
‘Ύ![]() …œ‘ΥΕ· ±Θ§»γΆΦΔΎΘ°ΙΐΒψ
…œ‘ΥΕ· ±Θ§»γΆΦΔΎΘ°ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§¥ΙΉψΈΣ
÷αΘ§¥ΙΉψΈΣ![]() Θ§
Θ§![]() Θ§¥ΙΉψΈΣ
Θ§¥ΙΉψΈΣ![]() Θ°…ηΨΊ–Έ
Θ°…ηΨΊ–Έ![]() ”κ
”κ![]() ÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣ
÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣ![]() Θ§«σ
Θ§«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ω
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ω![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®4Θ©Βψ![]() ΈΣ
ΈΣ![]() ÷α…œ“ΜΒψΘ§÷±œΏ
÷α…œ“ΜΒψΘ§÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ° «Ζώ¥φ‘ΎΒψ
Θ° «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΖϊΚœΧθΦΰΒΡΥυ”–
ΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΖϊΚœΧθΦΰΒΡΥυ”–![]() ΒψΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒψΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
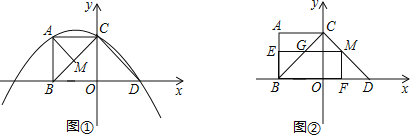
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ‘ΥΕ·Μα«ΑœΠΘ§ΙβΟς÷–―ßΕΦΜαΙΚ¬ράΚ«ρΓΔΉψ«ρΉςΈΣΫ±ΤΖΘ°»τΙΚ¬ρ6ΗωάΚ«ρΚΆ8ΗωΉψ«ρΙ≤Μ®Ζ―1700‘ΣΘ§«“ΙΚ¬ρ“ΜΗωάΚ«ρ±»ΙΚ¬ρ“ΜΗωΉψ«ρΕύΜ®50‘ΣΘ°
Θ®1Θ©«σΙΚ¬ρ“ΜΗωάΚ«ρΘ§“ΜΗωΉψ«ρΗς–ηΕύ…Ό‘ΣΘΜ
Θ®2Θ©ΫώΡξ―ß–ΘΦΤΜ°ΙΚ¬ρ’β÷÷άΚ«ρΚΆΉψ«ρΙ≤10ΗωΘ§«ΓΖξ…Χ≥Γ‘Ύ¥ΌœζΜνΕ·Θ§άΚ«ρ¥ρΨ≈’έΘ§Ήψ«ρ¥ρΑΥΈε’έΘ§»τ¥Υ¥ΈΙΚ¬ρΝΫ÷÷«ρΒΡΉήΖ―”Ο≤Μ≥§Ιΐ1150‘ΣΘ§‘ρΉνΕύΩ…ΙΚ¬ρΕύ…ΌΗωΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―«÷όΈΡΟςΕ‘ΜΑ¥σΜα’ΌΩΣΤΎΦδΘ§¥σ≈ζΒΡ¥σ―ß…ζ÷Ψ‘Η’Ώ≤Έ”κΖΰΈώΙΛΉς.Ρ≥¥σ―ßΦΤΜ°Ήι÷·±Ψ–Θ»ΪΧε÷Ψ‘Η’ΏΆ≥“Μ≥Υ≥Β»ΞΜα≥ΓΘ§»τΒΞΕάΒς≈δ36Ήυ–¬Ρή‘¥ΩΆ≥Β»τΗ…ΝΨΘ§‘ρ”–2»ΥΟΜ”–ΉυΈΜΘΜ»τ÷ΜΒς≈δ22Ήυ–¬Ρή‘¥ΩΆ≥ΒΘ§‘ρ”Ο≥Β ΐΝΩΫΪ‘ωΦ”4ΝΨΘ§≤ΔΩ’≥ω2ΗωΉυΈΜ.
(1)ΦΤΜ°Βς≈δ36Ήυ–¬Ρή‘¥ΩΆ≥ΒΕύ…ΌΝΨΘΩΗΟ¥σ―ßΙ≤”–Εύ…ΌΟϊ÷Ψ‘Η’ΏΘΩ
(2)»τΆ§ ±Βς≈δ36ΉυΚΆ22ΉυΝΫ÷÷≥Β–ΆΘ§Φ»±Θ÷ΛΟΩ»Υ”–ΉυΘ§”÷±Θ÷ΛΟΩ≥Β≤ΜΩ’ΉυΘ§‘ρΝΫ÷÷≥Β–ΆΗς–ηΕύ…ΌΝΨΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ«λΉΘ÷–ΜΣ»ΥΟώΙ≤ΚΆΙζΤΏ °÷ήΡξΜΣΒ°Θ§Ρ≥–ΘΨΌ–– ιΜ≠¥σ»ϋΘ§ΉΦ±ΗΙΚ¬ρΦΉΓΔ““ΝΫ÷÷ΈΡΨΏΘ§Ϋ±άχ‘ΎΜνΕ·÷–±μœ÷”≈–ψΒΡ Π…ζΘ°“―÷ΣΙΚ¬ρ![]() ΗωΦΉ÷÷ΈΡΨΏΓΔ
ΗωΦΉ÷÷ΈΡΨΏΓΔ![]() Ηω““÷÷ΈΡΨΏΙ≤–ηΜ®Ζ―
Ηω““÷÷ΈΡΨΏΙ≤–ηΜ®Ζ―![]() ‘ΣΘΜΙΚ¬ρ
‘ΣΘΜΙΚ¬ρ![]() ΗωΦΉ÷÷ΈΡΨΏΓΔ
ΗωΦΉ÷÷ΈΡΨΏΓΔ![]() Ηω““÷÷ΈΡΨΏΙ≤–ηΜ®Ζ―
Ηω““÷÷ΈΡΨΏΙ≤–ηΜ®Ζ―![]() ‘ΣΘ°
‘ΣΘ°
Θ®1Θ©«σΙΚ¬ρ“ΜΗωΦΉ÷÷ΈΡΨΏΓΔ“ΜΗω““÷÷ΈΡΨΏΗς–ηΕύ…Ό‘ΣΘΩ
Θ®2Θ©»τ―ß–ΘΦΤΜ°ΙΚ¬ρ’βΝΫ÷÷ΈΡΨΏΙ≤![]() ΗωΘ§ΆΕ»κΉ Ϋπ≤Μ…Ό”Ύ
ΗωΘ§ΆΕ»κΉ Ϋπ≤Μ…Ό”Ύ![]() ‘Σ”÷≤ΜΕύ”Ύ
‘Σ”÷≤ΜΕύ”Ύ![]() ‘ΣΘ§…ηΙΚ¬ρΦΉ÷÷ΈΡΨΏ
‘ΣΘ§…ηΙΚ¬ρΦΉ÷÷ΈΡΨΏ![]() ΗωΘ§«σ”–Εύ…Ό÷÷ΙΚ¬ρΖΫΑΗΘΩ
ΗωΘ§«σ”–Εύ…Ό÷÷ΙΚ¬ρΖΫΑΗΘΩ
Θ®3Θ©…η―ß–ΘΆΕ»κΉ Ϋπ![]() ‘ΣΘ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΡΡ÷÷ΙΚ¬ρΖΫΑΗ–η“ΣΒΡΉ ΫπΉν…ΌΘΩΉν…ΌΉ Ϋπ «Εύ…Ό‘ΣΘΩ
‘ΣΘ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΡΡ÷÷ΙΚ¬ρΖΫΑΗ–η“ΣΒΡΉ ΫπΉν…ΌΘΩΉν…ΌΉ Ϋπ «Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com