Question

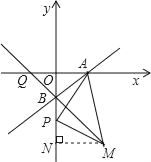
【题目】已知：如图，平面直角坐标系xOy中，点A、B的坐标分别为A（2，0），B（0，﹣2），P为y轴上B点下方一点，以AP为边作等腰直角三角形APM，其中PM＝PA，点M落在第四象限，过M作MN⊥y轴于N．

（1）求直线AB的解析式；

（2）求证：△PAO≌△MPN；

（3）若PB＝m（m＞0），用含m的代数式表示点M的坐标；

（4）求直线MB的解析式．

Answer 1

【答案】（1）y＝x﹣2．（2）详见解析；（3）（2+m，﹣4﹣m）；（4）y＝﹣x﹣2．

【解析】

（1）直线AB的解析式为y＝kx+b（k≠0），利用待定系数法求函数的解析式即可；

（2）先证∠APO＝∠PMN，用AAS证△PAO≌△MPN；

（3）由（2）中全等三角形的性质得到OP＝NM，OA＝NP．根据PB＝m，用m表示出NM和ON＝OP+NP，根据点M在第四象限，表示出点M的坐标即可．

（4）设直线MB的解析式为y＝nx﹣2，根据点M（m+2，﹣m﹣4）．然后求得直线MB的解析式．

（1）解：设直线AB：y＝kx+b（k≠0）

代入A（2，0 ），B （0，﹣2 ），得

，

解得，

∴直线AB的解析式为：y＝x﹣2．

（2）证明：作MN⊥y轴于点N．

∵△APM为等腰直角三角形，PM＝PA，

∴∠APM＝90°．

∴∠OPA+∠NPM＝90°．

∵∠NMP+∠NPM＝90°，

∴∠OPA＝∠NMP．

在△PAO与△MPN中

，

∴△PAO≌△MPN（AAS）．

（3）由（2）知，△PAO≌△MPN，则OP＝NM，OA＝NP．

∵PB＝m（m＞0），

∴ON＝2+m+2＝4+m MN＝OP＝2+m．

∵点M在第四象限，

∴点M的坐标为（2+m，﹣4﹣m）．

（4）设直线MB的解析式为y＝nx﹣2（n≠0）．

∵点M（2+m，﹣4﹣m）．

在直线MB上，

∴﹣4﹣m＝n（2+m）﹣2．

整理，得（m+2）n＝﹣m﹣2．

∵m＞0，

∴m+2≠0．

解得 n＝﹣1．

∴直线MB的解析式为y＝﹣x﹣2．