

| A. | 309 | B. | 316 | C. | 336 | D. | 339 |
分析 由于在此道路上距离A地12公里处设置第一个广告牌,之后每往东27公里就设置一个广告牌,所以第n个广告牌距离A地12+27(n-1),设此车停止时前面有x个广告牌,根据题意列出不等式12+27(x-1)≤320+19,将不等式的最大整数解代入12+27(x-1),计算即可.
解答 解:设此车停止时前面有x个广告牌,根据题意得
12+27(x-1)≤320+19,
x≤13$\frac{3}{27}$,
即此车停止时前面有13个广告牌,并且超过第13个广告牌3公里,
所以此车在停止前经过的最后一个广告牌距离A地320+19-3=336公里.
故选C.
点评 本题考查了一元一次不等式的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的不等关系列出不等式,再求解.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
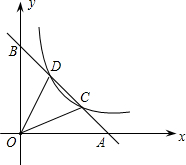 如图,直线l过点A(a,0)和点B(0,b)(其中a>0,b>0).反比例函数y=$\frac{k}{x}$(k>0)的图象与直线l交于C、D两点,连接OC、OD.
如图,直线l过点A(a,0)和点B(0,b)(其中a>0,b>0).反比例函数y=$\frac{k}{x}$(k>0)的图象与直线l交于C、D两点,连接OC、OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
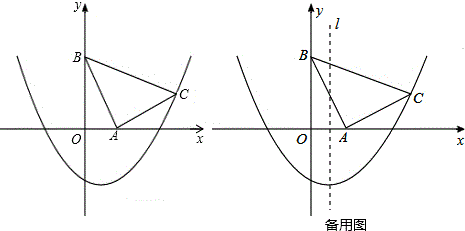
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
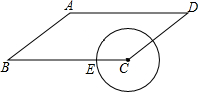 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 3<CE≤8 | D. | 3<CE≤5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com