
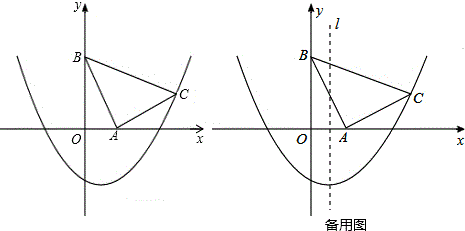
���� ��1������C��CD��x���ڵ�D�����ݡ�AOB�ա�CDA���CD��OD�ó�C��3��1�����ٴ���������y=$\frac{1}{2}$x2+bx-2���ɣ�
��2�������S��ABC�����ֱ��BC�Ľ���ʽΪy=-$\frac{1}{3}$x+2��ͬ�����ֱ��AC��AB�Ľ���ʽ����ֱ��l��x�ύ������Ϊ��x��0������ֱ��l��BC��AC�ֱ��ڵ�F��E������S��CEF=$\frac{1}{3}$S��ABC���ó�$\frac{1}{2}$��$\frac{5}{2}$-$\frac{5}{6}$x��•��3-x��=$\frac{1}{3}$��$\frac{5}{2}$�����x���ɣ���ֱ��l��BC��AB�ֱ��ڵ�F��E������S��BEF=$\frac{1}{3}$S��ABC��
�ó�$\frac{1}{2}$•$\frac{5}{3}$x•x=$\frac{1}{3}$��$\frac{5}{2}$���x���ɣ�
��3���ӳ�CB���������ڵ�P3������B����B��P1��BC�����������ڵ�P1��P2����ֱ��B��P1�Ľ���ʽΪ��y=-$\frac{1}{3}$x+b������B����B��M��x���ڵ�M��
���ݡ�AOB�ա�AMB�����B������꣬�ó�ֱ��B��P1�Ľ���ʽΪ��y=-$\frac{1}{3}$x-$\frac{4}{3}$���ٸ���$\left\{\begin{array}{l}{y=-\frac{1}{3}x-\frac{4}{3}}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}x-2}\end{array}\right.$�ó�P1��P2�����꣬����$\left\{\begin{array}{l}{y=-\frac{1}{3}x+2}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}x-2}\end{array}\right.$�ó�P3�����꣮
��� �⣺��1����ͼ1��ʾ������C��CD��x���ڵ�D�����CAD+��ACD=90�㣮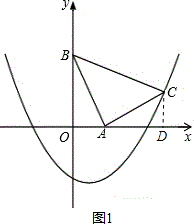
�ߡ�ABC�ǵ���ֱ�������Σ�
��AB=AC����BAC=90�㣬
���OAB+��CAD=90�㣬
���OAB=��ACD��
�ߡ�BOA=��ADC=90�㣬
�ڡ�AOB�͡�CDA�У�
$\left\{\begin{array}{l}{��OAB=��ACD}\\{��AOB=��ADC}\\{AB=AC}\end{array}\right.$��
���AOB�ա�CDA��AAS����
��CD=OA=1��AD=OB=2��
��OD=OA+AD=3��
��C��3��1����
�ߵ�C��3��1����������y=$\frac{1}{2}$x2+bx-2�ϣ�
��1=$\frac{1}{2}$��9+3b-2����ã�b=-?$\frac{1}{2}$��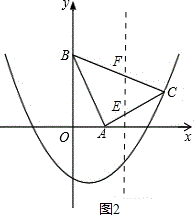
�������ߵĽ���ʽΪ��y=$\frac{1}{2}$x2-$\frac{1}{2}$x-2��
��2����Rt��AOB��
��OA=1��OB=2��
��AB=$\sqrt{5}$��
��S��ABC=$\frac{1}{2}$AB2=$\frac{5}{2}$��
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��0��2����C��3��1����
��$\left\{\begin{array}{l}{3k+b=1}\\{b=2}\end{array}\right.$��
���k=-$\frac{1}{3}$��b=2��
��y=-$\frac{1}{3}$x+2��
ͬ�����ֱ��AC�Ľ���ʽΪ��y=$\frac{1}{2}$x-$\frac{1}{2}$��
ֱ��AB�Ľ���ʽΪ��y=-2x+2��
��ֱ��l��x�ύ������Ϊ��x��0��
��ͼ2����ֱ��l��BC��AC�ֱ��ڵ�F��E����EF=��-$\frac{1}{3}$?x+2��-��$\frac{1}{2}$x-$\frac{1}{2}$��=$\frac{5}{2}$-$\frac{5}{6}$x��
��CEF�У�EF���ϵĸ�h=OD-x=3-x��
������ã�S��CEF=$\frac{1}{3}$S��ABC��
����$\frac{1}{2}$EF•h=$\frac{1}{3}$S��ABC��
��$\frac{1}{2}$��$\frac{5}{2}$-$\frac{5}{6}$x��•��3-x��=$\frac{1}{3}$��$\frac{5}{2}$��
���x1=3-$\sqrt{2}$��x2=3+?$\sqrt{2}$���������⣬��ȥ����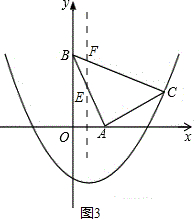 ��ͼ3����ֱ��l��BC��AB�ֱ��ڵ�F��E��
��ͼ3����ֱ��l��BC��AB�ֱ��ڵ�F��E��
��EF=��-$\frac{1}{3}$x+2��-��-2 x+2��=$\frac{5}{3}$x
��BEF�У�EF���ϵĸ�h=x��
������ã�S��BEF=$\frac{1}{3}$S��ABC��
����$\frac{1}{2}$EF•h=$\frac{1}{3}$S��ABC��$\frac{1}{2}$•$\frac{5}{3}$x•x=$\frac{1}{3}$��$\frac{5}{2}$
���x1=1��x2=-1���������⣬��ȥ��
��ֱ��l��x�ύ������Ϊ��1��0����3-$\sqrt{2}$��0��ʱ��ǡ�ý���ABC�������Ϊ1��2�������֣�
��3�����ڣ�
��ͼ4���ӳ�CB���������ڵ�P3������B����B��P1��BC�����������ڵ�P1��P2��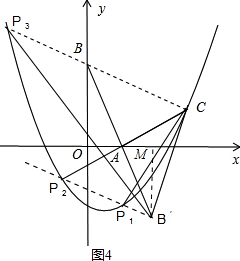 ��CB��B��P1��
��CB��B��P1��
��ֱ��B��P1�Ľ���ʽΪ��y=-$\frac{1}{3}$x+b��
����B����B��M��x���ڵ�M��
�ڡ�AOB�͡�AMB���У�
$\left\{\begin{array}{l}{��BAO=��B��AM}\\{��BOA=��AMB��}\\{AB=AB��}\end{array}\right.$��
���AOB�ա�AMB�䣨AAS����
��B��M=BO=2��
AM=AO=1��
��B���������2��-2����
��-2=-$\frac{1}{3}$��2+b��
��b=-$\frac{4}{3}$��
��ֱ��B��P1�Ľ���ʽΪ��y=-$\frac{1}{3}$x-$\frac{4}{3}$��
��$\left\{\begin{array}{l}{y=-\frac{1}{3}x-\frac{4}{3}}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}x-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=-\frac{16}{9}}\end{array}\right.$��
��P1�������ǣ�-1��-1����P2��������$��\frac{4}{3}��-\frac{16}{9}��$��
�ߡ�ACB=��ACB��=45�㣬
���B��CP3=90�㣬
��$\left\{\begin{array}{l}{y=-\frac{1}{3}x+2}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}x-2}\end{array}\right.$�ã�$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$����ȥ������$\left\{\begin{array}{l}{x=-\frac{8}{3}}\\{y=\frac{26}{9}}\end{array}\right.$��
��P3��������$��-\frac{8}{3}��\frac{26}{9}��$��
��P��������P1��-1��-1����P2$��\frac{4}{3}��-\frac{16}{9}��$��P3$��-\frac{8}{3}��\frac{26}{9}��$��
���� ���⿼���˶��κ����ۺϣ��õ���֪ʶ���Ƕ��κ�����ͼ�������ʡ�һ�κ�����ȫ�������ε��ж������ʣ��ؼ��Ǹ������⻭��ͼ�Σ�ע��������з��������ĵ㣮


 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
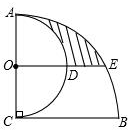 ��ͼ��AC��BC��AC=BC=2����ACΪֱ������Բ��Բ��Ϊ��O���Ե�CΪԲ�ģ�BCΪ�뾶����C������O��BC��ƽ���߽������ڵ�D��E������Ӱ���ֵ������$\frac{5}{12}$��-$\frac{1}{2}$$\sqrt{3}$��
��ͼ��AC��BC��AC=BC=2����ACΪֱ������Բ��Բ��Ϊ��O���Ե�CΪԲ�ģ�BCΪ�뾶����C������O��BC��ƽ���߽������ڵ�D��E������Ӱ���ֵ������$\frac{5}{12}$��-$\frac{1}{2}$$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{9}{10}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{1}{10}$ | D�� | $\frac{2}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ͼ������OCBD��ͼ��ʾ��OD=2��OC=3��������������ͼ����B����AΪ��һ����˫�����ϵĶ��㣨��B���⣩������A��AF��BD�ڵ�F��AE��x���ڵ�E��������OCBD�;���AEDF���ƣ����A�������ǣ�$\sqrt{5}$+1��$\frac{3\sqrt{5}-3}{2}$����$\sqrt{10}$+1��$\frac{2\sqrt{10}-2}{3}$����
��֪��ͼ������OCBD��ͼ��ʾ��OD=2��OC=3��������������ͼ����B����AΪ��һ����˫�����ϵĶ��㣨��B���⣩������A��AF��BD�ڵ�F��AE��x���ڵ�E��������OCBD�;���AEDF���ƣ����A�������ǣ�$\sqrt{5}$+1��$\frac{3\sqrt{5}-3}{2}$����$\sqrt{10}$+1��$\frac{2\sqrt{10}-2}{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 309 | B�� | 316 | C�� | 336 | D�� | 339 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2֮�� | B�� | 2��3֮�� | C�� | 3��4֮�� | D�� | 4��5֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com