
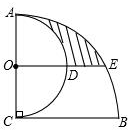
 如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$. 分析 如图,图中S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE.根据已知条件易求得OA=OC=OD=2,BC=CE=4.∠ECB=∠OEC=30°,所以由扇形面积公式、三角形面积公式进行解答即可.
解答 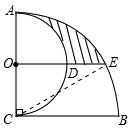 解:如图,连接CE.
解:如图,连接CE.
∵AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$,
∴∠ACB=90°,OA=OC=OD=1,BC=CE=2.
又∵OE∥BC,
∴∠AOE=∠COE=90°.
∴在直角△OEC中,OC=$\frac{1}{2}$CE,
∴∠OEC=30°,OE=$\sqrt{3}$.
∴∠ECB=∠OEC=30°,
∴S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE
=$\frac{90π×{2}^{2}}{360}$-$\frac{90π×{1}^{2}}{360}$-$\frac{30π×{2}^{2}}{360}$-$\frac{1}{2}$×1×$\sqrt{3}$
=$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
故答案为$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
点评 本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 11 | B. | 20 | C. | 41 | D. | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/台) | 售价(元/台) | |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空 调 | 2400 | 2700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com