
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=![]() +
+![]() ﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
【答案】(1)8;(2)点P的坐标为(0,4)或(0,﹣4);(3)比值不变.
【解析】
试题分析:(1)根据被开方数大于等于0列式求出b,再求出a,从而得到A、B的坐标,再根据向上平移纵坐标加,向右平移横坐标加求出点C、D的坐标即可,然后利用平行四边形的面积公式列式计算即可得解;
(2)根据三角形的面积公式列出方程求出OP,再分点P在y轴正半轴和负半轴两种情况讨论求解;
(3)根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE,然后求出∠CPO=∠DCP+∠BOP,从而判断出比值不变.
解:(1)由题意得,3﹣b≥0且b﹣3≥0,
解得b≤3且b≥3,
∴b=3,
a=﹣1,
∴A(﹣1,0),B(3,0),
∵点A,B分别向上平移2个单位,再向右平移1个单位,
∴点C(0,2),D(4,2);
∵AB=3﹣(﹣1)=3+1=4,
∴S四边形ABDC=4×2=8;
(2)∵S△PAB=S四边形ABDC,
∴![]() ×4OP=8,
×4OP=8,
解得OP=4,
∴点P的坐标为(0,4)或(0,﹣4);
(3)![]() =1,比值不变.
=1,比值不变.
理由如下:由平移的性质可得AB∥CD,
如图,过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
∴![]() =1,比值不变.
=1,比值不变.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)
(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
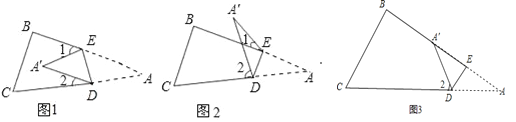
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,(如图3)则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要调查汇川区某所初中学校学生的平均体重,选取调查对象最合适的是( )
A. 选该校100名男生; B. 选该校100名女生;
C. 选该校七年级的两个班的学生; D. 在各年级随机选取100名学生。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空:
(a-b)(a+b)= ;
(a-b)(a2+ab+b2)= ;
(a-b)(a3+a2b+ab2+b3)= .
(2)猜想:
(a-b)(an-1+an-2b+…+abn-2+bn-1)= (其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:
29-28+27-…+23-22+2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com