
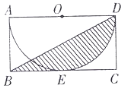
【题目】如图,在矩形ABCD中,BC=2,CD=1,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为__________.(结果保留![]() )
)
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.

(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,
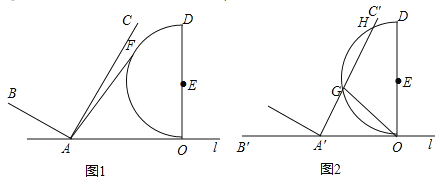
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为__________,最小值为__________;
的最大值为__________,最小值为__________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图2,若![]() 截半圆
截半圆![]() 的弧
的弧![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
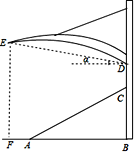
求:(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位长度为1的数轴上,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
![]()
(1)求![]() 的长;
的长;
(2)若把图中数轴的单位长度扩大30倍,点A,点B表示的数也相应发生变化,已知点P是线段![]() 的三等分点,求点P表示的数.
的三等分点,求点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击比赛,两人4次射击的成绩(单位:环)如下:
甲:8,6,9,9;
乙:7,8,9,8.
(1)请将下表补充完整:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 1.5 | ||
乙 | 8 | 8 |
(2)谁的成绩较稳定?为什么?
(3)分别从甲、乙两人的成绩中随机各选取一次,则选取的两个成绩之和为16环的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
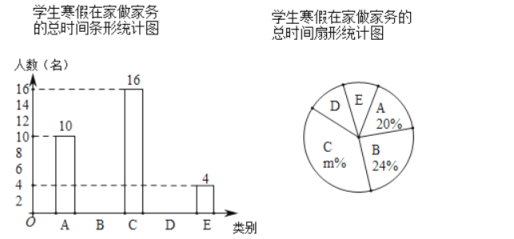
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,则下列四个结论中,错误的是( )
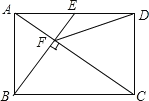
A. △AEF~△CABB. CF=2AFC. DF=DCD. tan∠CAD=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com