
����Ŀ����ͼ����֪������y=��x2+9�Ķ���ΪA������DE��˫����y= ![]() ��3��x��12����һ���֣�����G1 �� ��D��3��m����E��12��m��3������������y=��x2+9ˮƽ�����ƶ�a����λ���õ�������G2 ��
��3��x��12����һ���֣�����G1 �� ��D��3��m����E��12��m��3������������y=��x2+9ˮƽ�����ƶ�a����λ���õ�������G2 �� 
��1����˫���ߵĽ���ʽ��
��2����������y=��x2+9��x��Ľ���ΪB��C����B��C����࣬���߶�BD�ij�Ϊ��
��3���㣨6��n��ΪG1��G2�Ľ������꣬��a��ֵ��
��4���⣺���ƶ������У���G1��G2���������㣬��G2�ĶԳ���ֱ��߶�DE��G1��M��N���㣬��MN�� ![]() ��ֱ��д��a��ȡֵ��Χ��
��ֱ��д��a��ȡֵ��Χ��
���𰸡�
��1��
��D��3��m����E��12��m��3������y= ![]() ��
�� 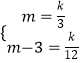 �����
����� ![]() ��
��
����˫���ߵĽ���ʽΪy= ![]() ��
��
��2��2 ![]()
��3��
�⣺�ѣ�6��n������y= ![]() ��6n=12�����n=2������������Ϊ��6��2����
��6n=12�����n=2��������������6��2����
������G2�Ľ���ʽΪy=����x��a��2+9��
�ѣ�6��2������y=����x��a��2+9�é���6��a��2+9=2�����a=6�� ![]() ��
��
��a��ֵΪ6�� ![]() ��
��
��4��
������G2�Ľ���ʽΪy=����x��a��2+9��
��D��3��4������y=����x��a��2+9���3��a��2+9=4�����a=3�� ![]() ��a=3+
��a=3+ ![]() ��
��
��E��12��1������y=����x��a��2+9���12��a��2+9=1�����a=12��2 ![]() ��a=12+2
��a=12+2 ![]() ��
��
��G1��G2���������㣬
��3+ ![]() ��a��12��2
��a��12��2 ![]() ��
��
��ֱ��DE�Ľ���ʽΪy=px+q��
��D��3��4����E��12��1������� ![]() �����
����� 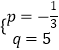 ��
��
��ֱ��DE�Ľ���ʽΪy=�� ![]() x+5��
x+5��
��G2�ĶԳ���ֱ��߶�DE��G1��M��N���㣬
��M��a���� ![]() a+5����N��a��
a+5����N��a�� ![]() ����
����
��MN�� ![]() ��
��
�ੁ ![]() a+5��
a+5�� ![]() ��
�� ![]() ��
��
������a2��13a+36��0������a��4����a��9����0��
��a��4��a��9��
��a��ȡֵ��ΧΪ9��a��12��2 ![]() ��
��
���������⣺��2����y=0ʱ����x2+9=0�����x1=��3��x2=3����B����3��0����
��D��3��4����
����BE= ![]() =2
=2 ![]() ��
��
���Դ���2 ![]() ��
��
�����㾫�������ڱ��⿼���ȷ��һ�κ����ı���ʽ�������ľ��룬��Ҫ�˽�ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ������ͬ����������룬���С����Ϊ֮������Ⱦ������㣬���������ˣ�ƽ�����������㣬���ݱ������ֵ�����ӿ�ƽ�������빫ʽҪ�μDz��ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��ACΪ��O���ң�AB=AC������AO��
��1����ͼl����֤����OAC=��OAB�� 
��2����ͼ2������B��AC�Ĵ��߽���O�ڵ�D������CD����AO���ӳ��߽�BD�ڵ�E����֤��BE=CD��
��3���ڣ�2���������£���ͼ3����F��G�ֱ���CD��BD���ӳ����ϣ�����AG��AF����CF��AG=8����GAB=45��+ ![]() ��GAE����B=50�㣬���ACF�������
��GAE����B=50�㣬���ACF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=8��AB=6����EΪ����DC��һ�����㣬�ѡ�ADE��AE�۵���ʹ��D���ڵ�F��������CEFΪֱ��������ʱ��DE�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵԱ���Ĺ����ɻ������ʡ���Ч���ʺ��乤����������ɣ����й��乤�ʵ��ƶ�����˿���Ա������ҵ��չ�Ĺ��ף�ͬʱ���Ա���Ļ����ԣ�����Ա���������ʣ��Ծ�����ְ����ѧ��Ա���ƶ����µĹ��乤�ʷ����� ���乤�ʷ�Ϊ��Ṥ�乤�ʺ���ҵ���乤�ʣ�
����Ṥ��=�μӱ���ҵ����ʱ���䩁18����ҵ����=�������䩁�μӱ���ҵ����ʱ���䣮
���깤��ʱ����뵱�깤��
������Ṥ�乤��y1��Ԫ/�£�����Ṥ��x���֮꣩��ĺ�����ϵʽ���ͼ��ʾ����ҵ���乤��y2��Ԫ/�£�����ҵ����x���֮꣩��ĺ�����ϵ��ͼ����ʾ��
������������
��1�����y1��y2�빤��x֮��ĺ�����ϵʽ��
��2������28��ĸ�����С�Ŵ�18����һֱʵ��ͬ�����乤���ƶȵ����ij��ҵ������Ϊ�˷����չ�������С��������С�Ż���ӦƸ������ҵ���Լ����һ�깤�乤��ÿ���½�����Ԫ��
��3���Ѿ��ڸ���ҵ��������3������ʦ����48�꣬��������Ĺ������ÿ�¶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ�����l1��l2�ƽ�У�A��B��l1�ϵ����㣬C��D��l2�ϵ����㣬ij���ڵ�A����á�CAB=90�㣬��DAB=30�㣬����AB����ǰ��20�����E����E���߶�AB�ϣ�����á�DEB=60�㣬��C��D�����ľ��룮 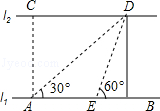
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ����ϣ���ʦ����ѧ��ȥ��һ���ϱ�����ĺӿ�����ͼ��ʾ��ijѧ���ںӶ�����A���۲�Ӷ�ˮ����һ��C�����C��A��ƫ��31��ķ����ϣ��غӰ���ǰ��20����B�������C��B��ƫ��45��ķ����ϣ���������������ݣ�������ͬѧ����������ӵĿ��ȣ����ο���ֵ��tan31��� ![]() ��sin31���
��sin31��� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����B������Ϊ��3��4����D��OA���е㣬��E��AB�ϣ�����CDE���ܳ���Сʱ����E������Ϊ�������� 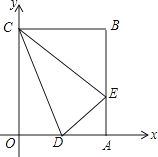
A.��3��1��
B.��3�� ![]() ��
��
C.��3�� ![]() ��
��
D.��3��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ������Ϊ60cm������Ϊ120��ĵ�����������ƤOAB�м���һ����������OCD���ô˼��µ�������ƤΧ��һ��Բ�IJ��棨������ģ������Բ�ĸ�Ϊ�������� 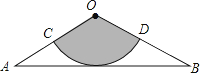
A.10cm
B.15cm
C.10 ![]() cm
cm
D.20 ![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͬ��Բ����Բ����AB��СԲ�����ڵ�P����Բ����CD������P����CD=13��PD=4������Բ��ɵ�Բ��������ǣ� �� 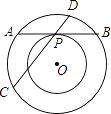
A.16��
B.36��
C.52��
D.81��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com