
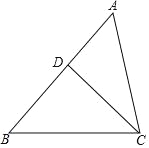
【题目】如图,△ABC中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=![]() ,点P为CD上一动点,当BP+
,点P为CD上一动点,当BP+![]() CP最小时,DP= .
CP最小时,DP= .
【答案】5![]() .
.
【解析】
试题分析:如图,作PE⊥AC于E,BE′⊥AC于E′交CD于P′.

∵CD⊥AB,∠ACD=30°,∠PEC=90°,AC=8,
∴PE=![]() PC,∠A=60°,∠ABE′=30°,AD=4,CD=4
PC,∠A=60°,∠ABE′=30°,AD=4,CD=4![]() ,
,
∴PB+![]() PC=PB+PE,
PC=PB+PE,
∴当BE′⊥AC时,PB+PE=BP′+P′E′=BE′最小,
∵tan∠ACB=![]() =
=![]() ,设BE′=5
,设BE′=5![]() ,CE′=3k,
,CE′=3k,
∴AE′=8﹣3k,AB=16﹣6k,BD=16﹣6k﹣4=12﹣6k,
∴BC2=BD2+CD2=BE′2+CE′2,
∴(12﹣6k)2+48=9k2+75k2,
整理得k2+3k﹣4=0,
∴k=1或﹣4(舍弃),
∴BE′=5![]() ,
,
∴PB+![]() PC的最小值为5
PC的最小值为5![]() .
.


科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒. 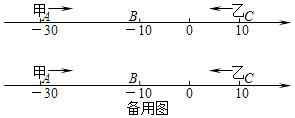
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
(1)求这个小组的男生达标率是多少?
(2)求这个小组8名男生的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
(1)当t=2时,求S的值;
(2)若S<5时,求t的取值范围.
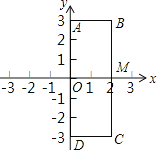
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() ﹣2kx+
﹣2kx+![]() +2=2(1﹣x)有两个实数根
+2=2(1﹣x)有两个实数根![]() ,
,![]() ,
,
(1)求实数k的取值范围;
(2)若方程的两实根![]() ,
,![]() 满足|
满足|![]() |=
|=![]() ﹣1,求k的值.
﹣1,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com