
【题目】如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
(1)当t=2时,求S的值;
(2)若S<5时,求t的取值范围.
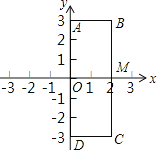
【答案】(1)S=5;(2)1.5<t<2或3<t<4
【解析】试题分析:设![]() 的面积为
的面积为![]()
![]() 的面积为则
的面积为则![]()
![]() 当t=2时,点P(0,2),Q(1,3),过点Q作QE⊥x轴于点
当t=2时,点P(0,2),Q(1,3),过点Q作QE⊥x轴于点![]() .根据三角形的面积公式分别求出
.根据三角形的面积公式分别求出![]()
![]() 进而得出
进而得出![]() 的值;
的值;
![]() 设点
设点![]() 运动的路程为
运动的路程为![]() 则点
则点![]() 运动的路程为
运动的路程为![]() 分五种情况进行讨论:①
分五种情况进行讨论:①![]() ;②
;②![]() ③
③![]() ④
④![]() ⑤
⑤![]() 针对每一种情况,首先确定出对应范围内点
针对每一种情况,首先确定出对应范围内点![]() 的位置,再根据三角形的面积公式求解即可.
的位置,再根据三角形的面积公式求解即可.
试题解析:设![]() 的面积为
的面积为![]()
![]() 的面积为
的面积为![]() 则
则![]()
(1)当t=2时,点P(0,2),Q(1,3),过点Q作QE⊥x轴于点![]() .
.
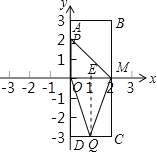
![]()
![]()
![]()
(2)设点P运动的路程为t,则点Q运动的路程为2t.
①当![]() 时,点P在线段OA上,点Q在线段OD上,
时,点P在线段OA上,点Q在线段OD上,
此时四边形OPMQ不存在,不合题意,舍去.
②当![]() 时,点P在线段OA上,点Q在线段DC上,
时,点P在线段OA上,点Q在线段DC上,
![]()
∵S<5,
∴t+3<5,解得t<2.
此时1.5<t<2.
③当![]() 时,点P在线段OA上,点Q在线段CM上,
时,点P在线段OA上,点Q在线段CM上,
![]()
∵S<5,
∴8t<5,解得t>3.
④当3<t<4时,点P在线段AB上,点Q在线段CM上,
![]()
∵S<5,
∴112t<5,解得t>3.
此时3<t<4.
⑤当t=4时,点P是线段AB的中点,点Q与M重合,两动点均停止运动,
此时四边形OPMQ不存在,不合题意,舍去.
综上所述,当S<5时,1.5<t<2或3<t<4.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
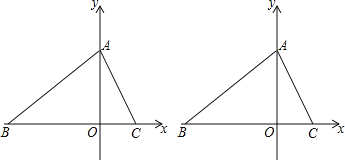
【题目】如图,在平面直角坐标系中,O为坐标原点.三角形ABC的边BC在石轴上,点B的坐标是(-5,0),点A在y轴的正半轴上,点C在x轴的正半轴上,它们的坐标分别为A(0,m)、C(m-1,0),且OA+OC=7,动点P从点B出发,以每秒2个单位的速度,沿射线BO运动.设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连结PA,当P沿射线BO匀速运动时,是否存在某一时刻,使三角形POA的面积是三角形ABC面积的![]() ?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.
?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
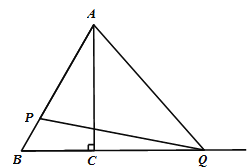
【题目】如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F. 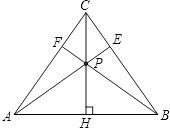
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记△ABC和△ABG的面积分别为S△ABC和S△ABG , 如果存在点P,能使得S△ABC=S△ABG , 求∠ACB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°, ∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒2个单位的速度运动,当点P到达点B时,P、Q同时停止运动,连结PQ、QA.设点P运动的时间为t秒.
(1)当CQ=2BP时,求t的值;
(2)当t为何值时QP=QA;
(3)若线段PQ的中垂线与线段BC相交(包括线段的端点),则t的取值范围是 .(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com