
����Ŀ����ͼ���ڵ�����ABC�У�CH�ǵױ��ϵĸ��ߣ���P���߶�CH�ϲ���˵��غϵ�����һ�㣬����AP��BC�ڵ�E������BP��AC�ڵ�F�� 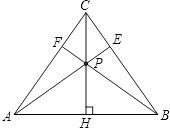
��1��֤������CAE=��CBF��
��2��֤����AE=BF��
��3�����߶�AE��BF��ABΪ�߹���һ���µ�������ABG����E���F�غ��ڵ�G�����ǡ�ABC�͡�ABG������ֱ�ΪS��ABC��S��ABG �� ������ڵ�P����ʹ��S��ABC=S��ABG �� ���ACB��ȡֵ��Χ��
���𰸡�
��1��֤�����ߡ�ABC�ǵ��������Σ�CH�ǵױ��ϵĸ��ߣ�
��AC=BC����ACP=��BCP��
�֡�CP=CP��
���ACP�ա�BCP��
���CAP=��CBP������CAE=��CBF��
��2��֤�������ڡ�ACE���BCF�У�
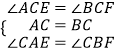 ��
��
���ACE�ա�BCF��ASA����
��AE=BF��
��3���⣺���ɣ�2��֪��ABG����ABΪ�ױߵĵ��������Σ�
��S��ABC=S��ABG��
��AE=AC��
�ٵ���ACBΪֱ�ǻ�۽�ʱ���ڡ�ACE�У����۵�P��CH�δ�������AE��AC�����Խ��۲�������
�ڵ���ACBΪ���ʱ����CAH=90�㩁 ![]() ��ACB������CAE����CAH��ҪʹAE=AC��ֻ��ʹ��ACB=��CEA��
��ACB������CAE����CAH��ҪʹAE=AC��ֻ��ʹ��ACB=��CEA��
��ʱ����CAE=180�㩁2��ACB��
ֻ��180�㩁2��ACB��90�㩁 ![]() ��ACB��
��ACB��
��ã�60�㣼��ACB��90�㣮
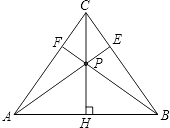
����������1��֤�á�ACP�ա�BCP���ɣ���2�����ϣ�1���Ľ��ۣ�֤�á�ACE�ա�BCF���ɣ���3��������ڵ�P����ʹ��S��ABC=S��ABG �� �ɣ�2���õ���AE=BF������������ABGҲΪ���������Σ����ݵױ߶�ΪAB�������ȣ��õ�����ȣ�����AC=AE����������ACEΪ���������Σ���ǡ�ACBΪ��ǣ����ɵõ���ACB��ȡֵ��Χ��
�����㾫�������ڱ��⿼��ĵ��������ε����ʣ���Ҫ�˽���������ε���������ȣ���ƣ��ȱ߶ԵȽǣ����ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y=![]() x2��bx+c��x�ύ�ڵ�A��8��0����B��2��0�����㣬��y�ύ�ڵ�C��
x2��bx+c��x�ύ�ڵ�A��8��0����B��2��0�����㣬��y�ύ�ڵ�C��
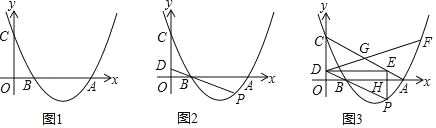
��1����ͼ1���������ߵĽ���ʽ��
��2����ͼ2����PΪ����������������һ�㣬����PB���ӳ���y���ڵ�D������P�ĺ�����Ϊt��CD��Ϊd����d��t�ĺ�����ϵʽ��������Ա���t��ȡֵ��Χ����
��3����ͼ3���ڣ�2���������£�����AC������P��PH��x�ᣬ����Ϊ��H���ӳ�PH��AC�ڵ�E������DE������DP����DE�ԳƵ�����DG��AC�ڵ�G���ӳ�DG���������ڵ�F������GΪAC�е�ʱ�����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ԭ��ΪO����A��0��3����B��2��3����C��2����3����D��0����3������P��Q�dz�����ABCD���ϵ��������㣬BC��x���ڵ�M����P�ӵ�O������ÿ��1����λ������O��A��B��M��·���������˶���ͬʱ��QҲ�ӵ�O������ÿ��2����λ������O��D��C��M��·���������˶�������Q�˶�����Mʱ���������ֹͣ�˶������˶���ʱ��Ϊt�룬�ı���OPMQ�����ΪS��
��1����t��2ʱ����S��ֵ��
��2����S��5ʱ����t��ȡֵ��Χ��
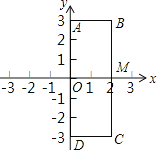
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�涨һ�������㣺x��y��xy+1��x��y��x+y��1�����磺2��3��2��3+1��7��2��3��2+3��1��4����a����4��5����ֵΪ17����a��x��a��6����x��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. a3a2��a5B. a2+2a2��3a4C. a6��a2��a3D. ��a3��2��a5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������M��y���ϵ���������ֱ��y=x+1�ཻ��A��B���㣬�ҵ�A��x���ϣ���B�ĺ�����Ϊ2������AM��BM��
��1���������ߵĺ�����ϵʽ��
��2���ж���ABM����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ��е���Ϊ10Ԫ��15Ԫ��20Ԫ�������ľߺг��ۣ����̵�ͳ����2014��3�·��������ľߺе����������������ͳ��ͼ�������������£� 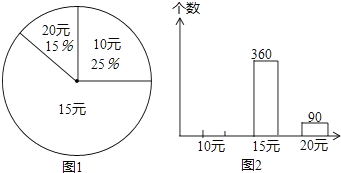
��1����ε�����һ����ȡ�˶��ٸ��ľߺУ�
��2�����ͼ1�б�ʾ��15Ԫ����������ռԲ�ĽǵĶ�����
��3����ͼ2�а�����ͳ��ͼ����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com