
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量 | 单价 |
不超过12 m3的部分 | a元∕m3 |
超过12 m3但不超过20 m3的部分 | 1.5a元∕m3 |
超过20 m3的部分 | 2a元∕m3 |
(1) 当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2) 设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费_____________元(用含a、n的整式表示);
(3) 当a=2时,甲、乙两用户一个月共用水40 m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
【答案】(1)80;(2)2an-16a;(3)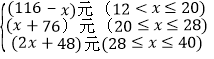
【解析】
分别计算出12m3,按a元/m3收费,超过12 m3但不超过20 m3的部分,按1.5a元/m3收费,超过20m3,按2a元/m3收费,然后计算三部分的和即可求解.
(1)2×12+2×1.5×(20-12)+2×2×(28-20)=80元
答:该用户这个月应缴纳80元水费
(2) 2an-16a
(3)∵甲用户缴纳的水费超过了24元
∴x>12
①12<x≤20
甲:2×12+3×(x-12)=3x-12
乙:20≤40-x<28
12×2+8×3+4×(40-x-20)=128-4x
共计:3x-12+128-40x=116-x
②20≤x≤28
甲:2×12+3×8+4(x-20)=4x-32
乙:12≤40-x≤20
2×12+3×(40-x-12)=108-3x
共计:4x-32+108-3x=x+76
③28≤x≤40
甲:2×12+3×8+4×(x-20)=4x-32
乙:0≤40-x≤12
2×(40-x)=80-2x
共计:4x-32+80-2x=2x+48
答:甲、乙两用户共缴纳的水费为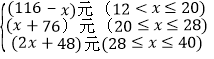 .
.
故答案为:(1)80;(2)2an-16a;(3)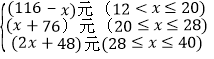 .
.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且![]() ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);
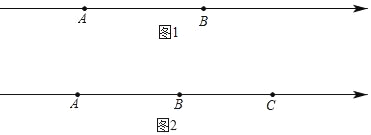
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(﹣20);
(2)(﹣8)﹣(﹣1);
(3)|﹣10|+|+8|;
(4)(﹣12)﹣5+(﹣14)﹣(﹣39);
(5)0.47﹣4![]() ﹣(﹣1.53)﹣1
﹣(﹣1.53)﹣1![]() ;
;
(6)36﹣76+(﹣23)﹣105;
(7)﹣20+|﹣14|﹣(﹣18)﹣13;
(8)(+1.75)+(﹣![]() )+(+
)+(+![]() )+(+1.05)+(﹣
)+(+1.05)+(﹣![]() )+(+2.2).
)+(+2.2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣![]() 的系数为﹣2;
的系数为﹣2;
(4)一个有理数不是整数就是分数
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
|
用水量(吨) |
|
|
|
|
|
费用(元) |
|
|
|
|
|
根据表格中提供的信息,回答以下问题:
![]() 求出规定吨数和两种收费标准;
求出规定吨数和两种收费标准;
![]() 若小明家
若小明家![]() 月份用水
月份用水![]() 吨,则应缴多少元?
吨,则应缴多少元?
![]() 若小明家
若小明家![]() 月份缴水费
月份缴水费![]() 元,则
元,则![]() 月份用水多少吨?
月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣ ![]() x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com