
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)和B(m,0),且3<m<4,则下列说法:①b<0;②a+c=b;③b2>4ac;④2b>3c;⑤![]() =1,正确的是( )
=1,正确的是( )

A.①②④B.①③⑤C.②③④D.②③⑤
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成,长方形OABC的长是12m,宽是4m,按照图中所示的平面直角坐标系,抛物线可以用y=﹣![]() x2+2x+c表示.
x2+2x+c表示.
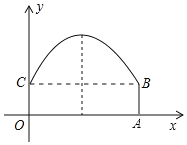
(1)请写出该抛物线的函数关系式;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:方程cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程.
(1)已知x=2是x2+2x+c=0的倒方程的解,求c的值;
(2)若一元二次方程ax2﹣2x+c=0无解,求证:它的倒方程也一定无解;
(3)一元二次方程ax2﹣2x+c=0(a≠c)与它的倒方程只有一个公共解,它的倒方程只有一个解,求a和c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与y轴交于点C,连接AB,AC,BC.
两点,与y轴交于点C,连接AB,AC,BC.

![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 求证:AB平分
求证:AB平分![]() ;
;
![]() 抛物线的对称轴上是否存在点M,使得
抛物线的对称轴上是否存在点M,使得![]() 是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.
x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.
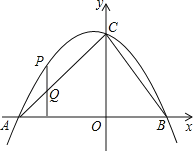
(1)求A,C两点的坐标.
(2)请用含a的代数式表示线段PQ的长,并求出a为何值时PQ取得最大值.
(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以B,C,Q为顶点的三角形是等腰三角形?若存在,请写出此时点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .抛物线上有一点
.抛物线上有一点![]() ,且
,且![]() .
.
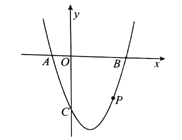
(1)求抛物线的解析式和顶点坐标.
(2)当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值.
面积的最大值.
(3)①设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .求
.求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,点
时,点![]() 的坐标是___________.
的坐标是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数![]() 的图象经过点C,一次函数
的图象经过点C,一次函数![]() 的图象经过点C,一次函数
的图象经过点C,一次函数![]() 的图象经过点A.
的图象经过点A.
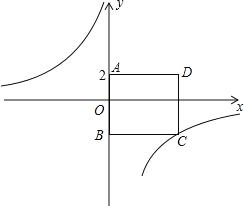
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数![]() 的图象上有且只有一个完美点
的图象上有且只有一个完美点![]() ,且当
,且当![]() 时,函数
时,函数![]() 的最小值为﹣3,最大值为1,则m的取值范围是( )
的最小值为﹣3,最大值为1,则m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com