
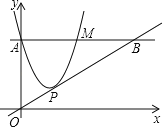
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+![]() (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为_____.
(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为_____.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A.其图象的对称轴为过![]() 且平行于
且平行于![]() 轴的直线.
轴的直线.
B.其最小值为1.
C.其图象与![]() 轴没有交点.
轴没有交点.
D.当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)如图所示,下列结论:①abc<0;②点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2;③b2>(a+c)2;④2a﹣b<0.正确的结论有( )
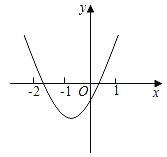
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数图象经过点A(2,2),B(m,3)
(1)求正比例函数的解析式及m的值;
(2)分别过点A与点B作y轴的平行线,与反比例函数在第一象限的分支分别交于点C、D(点C、D均在点A、B下方),若BD=4AC,求反比例函数的解析式;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
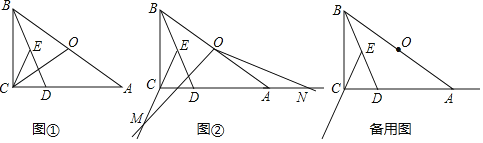
(1)如图①,连接OC,证明∠OCE=∠OAC;
(2)如图②,点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
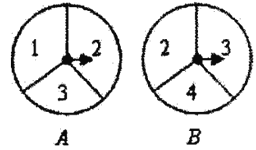
【题目】(1)方程![]() 的解是______________;
的解是______________;
(2)有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:①分别转动转盘A,B;②两个转盘停止后,观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).用列表法(或树状图)分别求出“两个指针所指的数字都是方程![]() 的解”的概率.
的解”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“万州古红桔”原名“万县红桔”,古称丹桔(以下简称为红桔),种植距今至少已有一千多年的历史,“玫瑰香橙”(源自意大利西西里岛塔罗科血橙,以下简称香橙)现已是万州柑橘发展的主推品种之一.某水果店老板在2017年11月份用15200元购进了400千克红桔和600千克香橙,已知香橙的每千克进价比红桔的每千克进价2倍还多4元.
(1)求11月份这两种水果的进价分别为每千克多少元?
(2)时下正值柑橘销售旺季,水果店老板决定在12月份继续购进这两种水果,但进入12月份,由于柑橘的大量上市,红桔和香橙的进价都有大幅下滑,红桔每千克的进价在11月份的基础上下降了![]() m%,香橙每千克的进价在11月份的基础上下降了m%,由于红桔和“玫瑰香橙”都深受库区人民欢迎,实际水果店老板在12月份购进的红桔数量比11月份增加了
m%,香橙每千克的进价在11月份的基础上下降了m%,由于红桔和“玫瑰香橙”都深受库区人民欢迎,实际水果店老板在12月份购进的红桔数量比11月份增加了![]() m%,香橙购进的数量比11月份增加了2m%,结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同,求m的值.
m%,香橙购进的数量比11月份增加了2m%,结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
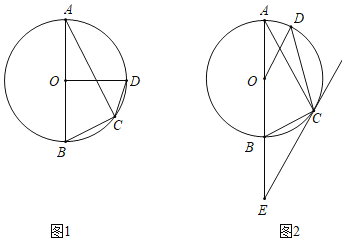
【题目】已知AB是⊙O的直径,C,D是⊙O上AB同侧两点,∠BAC=26°.
(Ⅰ)如图1,若OD⊥AB,求∠ABC和∠ODC的大小;
(Ⅱ)如图2,过点C作⊙O的切线,交AB的延长线于点E,若OD∥EC,求∠ACD的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com