
【题目】已知AB是⊙O的直径,C,D是⊙O上AB同侧两点,∠BAC=26°.
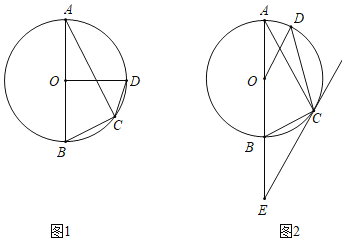
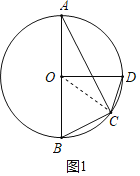
(Ⅰ)如图1,若OD⊥AB,求∠ABC和∠ODC的大小;
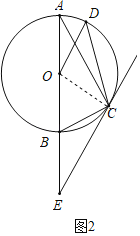
(Ⅱ)如图2,过点C作⊙O的切线,交AB的延长线于点E,若OD∥EC,求∠ACD的大小.
【答案】(Ⅰ)∠ABC=64°,∠ODC=71°;(Ⅱ)∠ACD=19°.
【解析】
(I)连接OC,根据圆周角定理得到∠ACB=90°,根据三角形的内角和得到∠ABC=65°,由等腰三角形的性质得到∠OCD=∠OCA+∠ACD=70°,于是得到结论;
(II)如图2,连接OC,根据圆周角定理和切线的性质即可得到结论.
解:(Ⅰ)连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=26°,
∴∠ABC=64°,
∵OD⊥AB,
∴∠AOD=90°,
∴∠ACD=![]() ∠AOD=
∠AOD=![]() ×90°=45°,
×90°=45°,
∵OA=OC,
∴∠OAC=∠OCA=26°,
∴∠OCD=∠OCA+∠ACD=71°,
∵OD=OC,
∴∠ODC=∠OCD=71°;
(Ⅱ)如图2,连接OC,
∵∠BAC=26°,
∴∠EOC=2∠A=52°,
∵CE是⊙O的切线,
∴∠OCE=90°,
∴∠E=38°,
∵OD∥CE,
∴∠AOD=∠E=38°,
∴∠ACD=![]() AOD=19°.
AOD=19°.


科目:初中数学 来源: 题型:
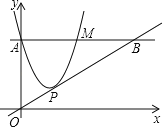
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+![]() (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为_____.
(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
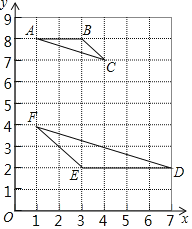
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)△ABC外接圆圆心的坐标为 ,半径是 ;
(2)已知△ABC与△DEF(点D、E、F都是格点)成位似图形,位似中心M的坐标是 ,△ABC与△DEF位似比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备采购一批茶艺耗材和陶艺耗材.经查询,如果按照标价购买两种耗材,当购买茶艺耗材的数量是陶艺耗材数量的2倍时,购买茶艺耗材共需要18000元,购买陶艺耗材共需要12000元,且一套陶艺耗材单价比一套茶艺耗材单价贵150元.
(1)求一套茶艺耗材、一套陶艺耗材的标价分别是多少元?
(2)学校计划购买相同数量的茶艺耗材和陶艺耗材.商家告知,因为周年庆,茶艺耗材的单价在标价的基础上降价2![]() 元,陶艺素材的单价在标价的基础降价150元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了2.5
元,陶艺素材的单价在标价的基础降价150元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了2.5![]() %和
%和![]() ,结果在结算时发现,两种耗材的总价相等,求
,结果在结算时发现,两种耗材的总价相等,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
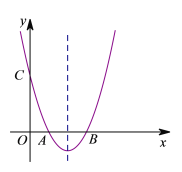
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),联结PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于![]() 轴的方向向下平移,平移后的抛物线的顶点为点D,点P关于x轴的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
轴的方向向下平移,平移后的抛物线的顶点为点D,点P关于x轴的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
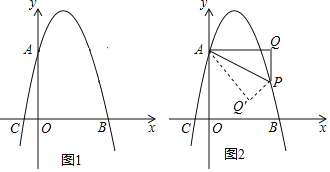
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元,若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买2件,所买的每件服装的售价均降低6元.已知该服装成本是每件200元.设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)顾客一次性购买多少件时,该网店从中获利最多,并求出获利的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
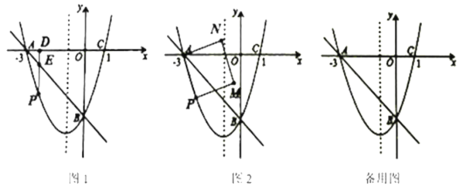
【题目】如图1,抛物线y = ax2+bx-3经过A、B、C三点,己知点A(-3,0)、C (1, 0).
(1)求此抛物线的解析式.
(2)点P是直线AB下方的抛物线上一动点(不与A、B重合),
①过点F作x轴的垂线,垂足为D,交直线AB于点E,动点P在什么位置时,PE最大,求 出此时P点的坐标.
②如图2,连接AP.以AP为边作图示一侧的正方形APMN,当它恰好有一个顶点落在抛物 线对称轴上时,求出对应的P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com