
分析 设腰长为x,底边长为y,根据等腰三角形一腰上的中线将这个等腰三角形的周长分为9和12两部分,列方程解得即可.
解答 解:设腰长为x,底边长为y,
则$\left\{\begin{array}{l}{x+\frac{x}{2}=12}\\{y+\frac{x}{2}=9}\end{array}\right.或\left\{\begin{array}{l}{x+\frac{x}{2}=9}\\{y+\frac{x}{2}=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=5}\end{array}\right.或\left\{\begin{array}{l}{x=6}\\{y=9}\end{array}\right.$,
经检验,都符合三角形的三边关系.
因此三角形的底边长为9cm或5cm,等腰三角形的腰长为6cm或8cm.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确3:2两部分是哪一部分含有底边,所以一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.


科目:初中数学 来源: 题型:解答题
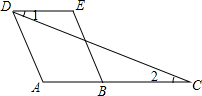 请将下列推理过程补充完整.
请将下列推理过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:选择题
矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
A.16 B.12 C.24 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
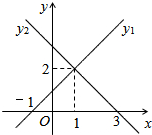 如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.
如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
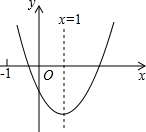 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com