
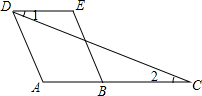
 请将下列推理过程补充完整.
请将下列推理过程补充完整. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
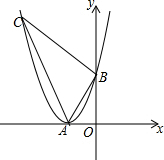 如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>5 | B. | m≥5 | C. | m<5 | D. | m≤5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
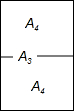 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 3:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.
已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
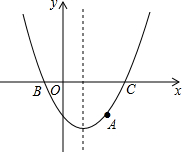
 已知二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-1,-5.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,若x1=1.3,则x2的值为( )
已知二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-1,-5.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,若x1=1.3,则x2的值为( )| A. | -1.3 | B. | -2.3 | C. | -0.3 | D. | -3.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
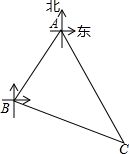 A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)
A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com