
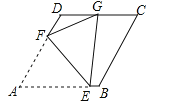
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= .
【答案】![]() .
.
【解析】
试题分析:延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,如图所示:
∵∠A=60°,四边形ABCD是菱形,∴∠MDF=60°,∴∠MFD=30°,设MD=x,则DF=2x,FM=![]() x,∵DG=1,∴MG=x+1,∴
x,∵DG=1,∴MG=x+1,∴![]() ,解得:x=0.3,∴DF=0.6,AF=1.4,∴AH=
,解得:x=0.3,∴DF=0.6,AF=1.4,∴AH=![]() AF=0.7,FH=AFsin∠A=1.4×
AF=0.7,FH=AFsin∠A=1.4×![]() =
=![]() ,∵CD=BC,∠C=60°,∴△DCB是等边三角形,∵G是CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG=
,∵CD=BC,∠C=60°,∴△DCB是等边三角形,∵G是CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG=![]() ,设BE=y,则GE=2﹣y,∴
,设BE=y,则GE=2﹣y,∴![]() ,解得:y=0.25,∴AE=1.75,∴EH=AE﹣AH=1.75﹣0.7=1.05,∴EF=
,解得:y=0.25,∴AE=1.75,∴EH=AE﹣AH=1.75﹣0.7=1.05,∴EF=![]() =
=![]() =
=![]() .故答案为:
.故答案为:![]() .
.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
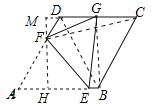
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,
然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= ![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,按此规律下去,则第n个菱形的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
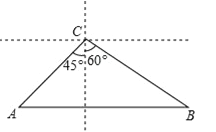
【题目】如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com