
����Ŀ�����գ�ij��ѧ�ٰ���һ���������ﴫͳ�Ļ���Ϊ����ĺ�����д��������һ�ͳ��������꼶����600��ѧ���μӣ�Ϊ�˸��õ��˽Ȿ�α����ɼ��ķֲ������ѧУ�ֱ�������꼶�����ȡ��������ѧ���ijɼ���Ϊ�������з����������������꼶ѧ���ɼ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������ÿ��������еķ���������ͷ֣���������߷֣�
����ѧ�������ɼ�Ƶ���ֲ��� | ||
����/�� | Ƶ�� | Ƶ�� |
50��60 | 2 | |
60��70 | 4 | 0.10 |
70��80 | 0.20 | |
80��90 | 14 | 0.35 |
90��100 | ||
�ϼ� | 40 | 1.00 |
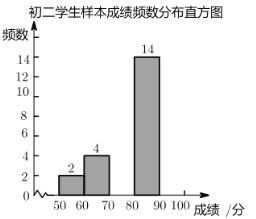
�����������Ϣ������������⣺
��1����ȫ�ɼ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
��2��������ѧ���ɼ�������80��90�ֶεľ���ɼ�Ϊ��
80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89
�ٸ���������Ϣ�����Ƴ���ѧ���ɼ�����λ��Ϊ__________��
������һѧ�������ɼ�����λ��Ϊ80����ͬѧ�ڱ����еõ���82�֣��������ڵ��꼶��λ��275��������������Ϣ�ƶϼ�ͬѧ�����꼶Ϊ__________��ѡ������һ������������������
�����ɼ���85�ּ����Ͼ�Ϊ����������������ݳ�ȡ���������ݣ����Ƴ����꼶ѧ���дﵽ����������ѧ������Ϊ__________�ˣ�
���𰸡���1��0.05��8��12��0.30����ͼ����������2����82.75���ڳ�һ����270
��������
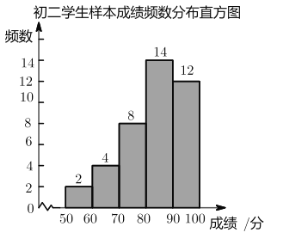
��1���������������Ƶ����Ƶ�ʣ����벢��ȫ�ɼ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���ɣ�
��2�����������֪��40��ѧ������λ��Ӧȡ��20�͵�21�����ݵ�ƽ���������з���������⣻
����������ó���ͬѧ�ijɼ����������꼶����λ������������꼶����λ�������бȽϷ�����
��������ó�80~90��һ������6��������85�ּ����ϣ�90~100��һ������12�����ݣ��ݴ˽��з�������.
�⣺��1��Ƶ��4��0.10��0.20=8��40-2-4-8-14=12��Ƶ��2��40=0.05��1-0.10-0.20-0.35-0��05=0.30��
����ѧ�������ɼ�Ƶ���ֲ��� | ||
����/�� | Ƶ�� | Ƶ�� |
50��60 | 2 | 0��05 |
60��70 | 4 | 0��10 |
70��80 | 8 | 0��20 |
80��90 | 14 | 0��35 |
90��100 | 12 | 0��30 |
�ϼ� | 40 | 1��00 |
��2������40��ѧ������λ��Ӧȡ��20�͵�21�����ݵ�ƽ������
50~60��60~70��70~80���������![]() ������
������
80~90��һ������14�����ݣ�
���ݾ���ɼ���֪����20������Ϊ82��5����21������Ϊ83��
������λ��Ϊ![]() ��
��
�ʴ�Ϊ��82.75��
�ڡ���һ�ͳ�������600��ͬѧ�μӣ�
��ͬѧλ�������꼶��275����
����ͬѧ�ijɼ����������꼶����λ����
����һ�꼶����λ��Ϊ80��
�����꼶����λ��Ϊ82��5��
��ͬѧ�ijɼ�Ϊ![]() ��
��
����ͬѧ�����꼶Ϊ��һ��
�ʴ�Ϊ����һ��
��80~90��һ������6��������85�ּ����ϣ�
90~100��һ������12�����ݣ�
���ɹ��Ƴ����꼶ѧ���дﵽ����������ѧ������Ϊ![]() ���ˣ���
���ˣ���
�ʴ�Ϊ��270��


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д� Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ����������ƽ�ȡ��ж�����г����ȡ������������ͻ��![]() ����������˳������飨ÿλͬѧֻѡ���ע��һ���������ݵ�����������������������ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
����������˳������飨ÿλͬѧֻѡ���ע��һ���������ݵ�����������������������ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
��1����ε����ѧ�����ж�������
��2���뽫����ͳ��ͼ������������������ͳ��ͼ�м��������ȡ������Ӧ��Բ�ĽǵĶ�����
��3�����Ҫ����![]() ����������ѡ�������е��飬���ݣ�2���е�����������״ͼ���б�������ǡ��ѡ��ѧ����ע������������ĸ��ʣ���������ƽ�ȡ��ж�����г����ȡ���μ�ΪA��B��C��D��E����
����������ѡ�������е��飬���ݣ�2���е�����������״ͼ���б�������ǡ��ѡ��ѧ����ע������������ĸ��ʣ���������ƽ�ȡ��ж�����г����ȡ���μ�ΪA��B��C��D��E����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
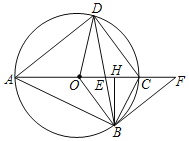
����Ŀ����ͼ���ı���ABCD�ڽ�����O��ֱ��AC����BD�Ľ���ΪE��OB��CD��BH��AC������ΪH���ҡ�BFA����DBC��
��1����֤��BF����O�����ߣ�
��2����BH��3����AD�ij��ȣ�
��3����sin��DAC��![]() �����OBH��������ı���OBCD�����֮�ȣ�
�����OBH��������ı���OBCD�����֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������п������ؿ���Ŀ֮һ��������ijѧУΪ�˽������꼶ѧ�������������������������ȡ���־��꼶ѧ����������IJ��Գɼ���Ϊһ����������A��B��C��D�ĸ��ȼ�����ͳ�ƣ��Ƴ������²�������ͳ��ͼ����˵����A����8�֩�10�֣�B����7�֩�7.9�֣�C����6�֩�6.9�֣�D����1�֩�5.9�֣�
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�C��Ӧ�����ε�Բ�Ľ����� ���ȣ�
��2����ȫ����ͳ��ͼ��
��3������ȡѧ��������������Գɼ�����λ���������� ���ȼ���
��4����У���꼶��300��ѧ�������������������Գɼ��ﵽA����ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��һ·��������������������ͨ��ͨ�š���Դ�ȸ�����ؽ���ȡ�û�����չ��ҲΪ�����������ڸ����ṩ���µķ�չ��������ͼ��2017����һ��һ·�����߲��ֹ��ҵ�ͨ����ʩ��״ͳ��ͼ��
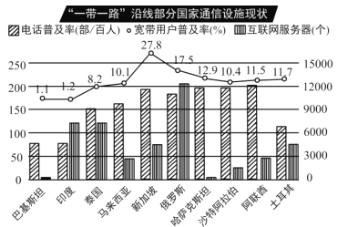
����ͳ��ͼ�ṩ����Ϣ�������ƶϺ������ǣ� ����
A.������������ӵ�и������Ĺ����ǰ�����
B.�����û��ռ��ʵ���λ����11.05%
C.��8�����ҵĵ绰�ռ����ܹ��ﵽƽ��ÿ��1��
D.ֻ�ж���˹������ָ�����������Ӧ����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ٰ��˶��ᣬ��1500����Ŀ�У�����ѡ����200�Ļ����ܵ��Ͻ��У���ͼ��¼���ܵ�����һλѡ����������һλѡ�ֵ��ܲ����̣�����ѡ��������ȫ�̣�������x��ʾ����ѡ�ֵ��ܲ�ʱ�䣬y��ʾ����λѡ��֮��ľ��룬��������4��˵������ȷ���У�������
������ѡ�ֵ����յ�ʱ��������ѡ�ֻ���15��δ�ܣ�
���ܵ�����ѡ����ʱ4'46�壻
������������ѡ����������ѡ�����������Σ�
������������ѡ����������ѡ�ֵ�һ�������ȵڶ�����������ʱ����
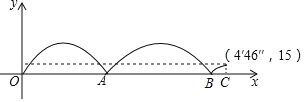
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() ����ƽ��
����ƽ��![]() ����λ��������ƽ��
����λ��������ƽ��![]() ����λ���õ�������
����λ���õ�������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��һ�������Ϊ
��һ�������Ϊ![]() ����
����![]() ��һ�������Ϊ
��һ�������Ϊ![]() ����
����![]() �������
�������![]() ����
����![]() �ڵ�һ�����ڣ�
�ڵ�һ�����ڣ�
��1�����![]() �����꼰
�����꼰![]() �ı���ʽ��
�ı���ʽ��
��2����![]() ���߶�
���߶�![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ��
��![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ����
����![]() ���Ҳ���������
���Ҳ���������![]() ��
��
�ٵ���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ʱ��ֱ��
ʱ��ֱ��![]() ǡ�þ���������
ǡ�þ���������![]() �Ķ���
�Ķ���![]() �����ʱ
�����ʱ![]() ��ֵ��
��ֵ��
���ڵ�![]() ���˶������У���ֱ��
���˶������У���ֱ��![]() ��������
��������![]() ʼ��û�й����㣬ֱ��д��
ʼ��û�й����㣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
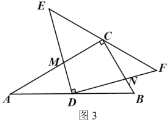
����Ŀ�����ٴ�أ�ѧУ��������12�ף���9��һ�鳤����չʾ��������ֲ�����ֽ��仮�ֳ���ͼ����������������ABCD���ֺ���������ܻ��β��֣�����������üס��ҡ������ֻ�����ֲ����EFƽ��BD��G��H�ֱ�ΪAB��CD�е㣮
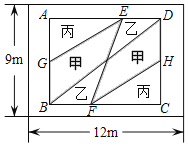
��1�������������ΪSm2����ֲ����Ϊ180Ԫ/m2�������IJ�ƺ����Ϊ40Ԫ/m2������������ܼ�Ϊ16500Ԫ����S��ֵ��
��2����AB��BC��4��5����������������ƺ������ȣ���Ϊ�ϡ��²�ƺ������2��
����AB��BC�ij���
�����ס������ۺ�Ϊ360Ԫ/m2���ҡ������۱�Ϊ13��12�����ֻ��ܵ��۾�Ϊ20����������������ABCD�л��ܵ���ֲ�ܼ�Ϊ14520Ԫʱ������ֲ�һ��ܵ��ܼۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
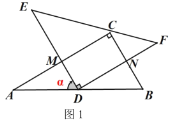
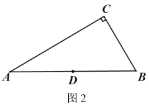
����Ŀ����֪����Rt��ABC��Rt��DEF�У���ACB=��EDF=90������A=30������E=45����AB=EF=6����ͼ1��D��б��AB���е㣬������Rt��DEF�Ƶ�D˳ʱ�뷽����ת������0��<��<90����������ת�����У�ֱ��DE��AC�ཻ�ڵ�M��ֱ��DF��BC�ཻ�ڵ�N��
��1����ͼ1������=60��ʱ����֤��DM=BN��
��2����������ת�����У�![]() ��ֵ��һ����ֵ������ͼ2�л���ͼ�β�����֤����
��ֵ��һ����ֵ������ͼ2�л���ͼ�β�����֤����
��3����ͼ3����������ת�����У�����C����б��EF��ʱ���������������غϲ����ı���CMDN�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com