
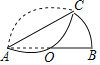
【题目】如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,![]() 恰好经过点O,则
恰好经过点O,则![]() 与
与![]() 的关系是
的关系是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:

我们把某一格中所有字母相加得到的多项式称为特征多项式,例如:第1格的“特征多项式”为x+4y.
回答下列问题:
⑴ 第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
⑵ 若第1格的“特征多项式”的值为2,第2格的“特征多项式”的值为-6.
① 求x,y的值;
② 在①的条件下,第n格的“特征多项式的值”随着n的变化而变化,求“特征多项式的值”的最大值及此时n值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
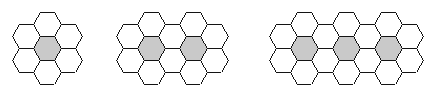
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:
![]()
![]()
![]()
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
查看答案和解析>>
科目:初中数学 来源: 题型:
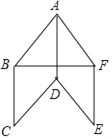
【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() (x>0)的图象上,点D的坐标为(4,3).设AB所在的直线解析式为
(x>0)的图象上,点D的坐标为(4,3).设AB所在的直线解析式为![]() ,若将菱形ABCD沿x轴正方向平移m个单位,
,若将菱形ABCD沿x轴正方向平移m个单位,
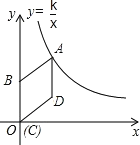
①当菱形的顶点B落在反比例函数的图象上,求m的值;
②在平移中,若反比例函数图象与菱形的边AD始终有交点,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
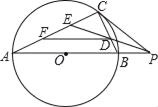
【题目】如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论正确的结论有 (填序号)
(1)△PBC∽△PCA (2)△PCD∽△PAE
(3)△CDE是等腰直角三角形 (4)点E、F三等分AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 、
、![]() 两点,分别代表-12、4.
两点,分别代表-12、4.
(1) ![]() 、
、![]() 两点间的距离为 个单位长度;
两点间的距离为 个单位长度;
(2)点![]() 从点
从点![]() 出发,以1个单位长度秒的速度沿数轴向点
出发,以1个单位长度秒的速度沿数轴向点![]() 做匀速运动,同时点
做匀速运动,同时点![]() 从点
从点![]() 出发,以3个单位长度/秒的速度沿数轴由
出发,以3个单位长度/秒的速度沿数轴由![]() →
→![]() →
→![]() 的路径做匀速运动,当点
的路径做匀速运动,当点![]() 最后到达
最后到达![]() 点时,都停止运动.设运动时间为
点时,都停止运动.设运动时间为![]() 秒
秒
①请写出![]() 时,
时,![]() 、
、![]() 两点相遇.
两点相遇.
②当![]() 时,两点停止运动.
时,两点停止运动.
③当![]() 时,求
时,求![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com