
【题目】如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.
(1)当∠DAE=45°时,求证:DE=D′E;
(2)在(1)得条件下,猜想:BD2、DE2、CE2有怎样的数量关系?请写出,并说明理由.
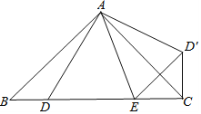
【答案】(1)证明见解析;(2)BD2+CE2=DE2.理由见解析
【解析】
(1)根据旋转的性质可得AD=AD′,∠CAD′=∠BAD,然后求出∠D′AE=45°,从而得到∠DAE=∠D′AE,再利用“边角边”证明△ADE和△AD′E全等,根据全等三角形对应边相等证明即可;
(2)由(1)知△AED≌△AED′得到:ED=ED′,由等腰直角三角形的性质可得AB=AC,∠BAC=90°,∠B=∠ACB=45°,再根据已知可得BD=CD′,∠B=∠ACD′=45°,继而可得∠BCD′=90°,在Rt△CD′E中,根据勾股定理有CE2+D′C2=D′E2,继而利用等量代换即可得BD2+CE2=DE2.
(1)∵△ABD绕点A旋转,得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°,
∵∠DAE=45°
∴∠EAD′=∠DAD′﹣∠DAE=90°﹣45°=45°,
∴∠EAD′=∠DAE,
在△AED与△AED′中
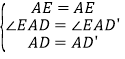 ,
,
∴△AED≌△AED′,
∴DE=D′E;
(2)BD2+CE2=DE2.理由如下:
由(1)知△AED≌△AED′得到:ED=ED′,
在△ABC中,AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵△ABD绕点A旋转,得到△ACD′
∴BD=CD′,∠B=∠ACD′=45°,
∴∠BCD′=∠ACB+∠ACD′=45°+45°=90°,
在Rt△CD′E中,CE2+D′C2=D′E2,
∴BD2+CE2=DE2.


科目:初中数学 来源: 题型:
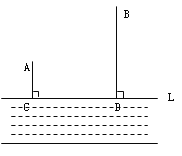
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
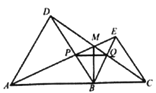
【题目】如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
查看答案和解析>>
科目:初中数学 来源: 题型:
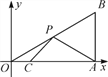
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() 的“矩面积”,给出如下定义:“水平底”
的“矩面积”,给出如下定义:“水平底”![]() 为任意两点横坐标差的最大值,“铅垂高”
为任意两点横坐标差的最大值,“铅垂高”![]() 为任意两点纵坐标差的最大值,则“矩面积”
为任意两点纵坐标差的最大值,则“矩面积”![]() .
.
例如:三点坐标分别为![]() ,则“水平底”
,则“水平底”![]() ,“铅垂高”
,“铅垂高”![]() ,“矩面积”
,“矩面积”![]() .
.
(1)已知点![]() .
.
①若![]() 三点的“矩面积”为12,求点
三点的“矩面积”为12,求点![]() 的坐标;
的坐标;
②求![]() 三点的“矩面积”的最小值.
三点的“矩面积”的最小值.
(2)已知点![]() ,其中
,其中![]() .若
.若![]() 三点的“矩面积”为8,求
三点的“矩面积”为8,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com