
ЁОЬтФПЁПЛЭМВЂЬжТлЃЎ

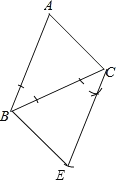
вбжЊІЄABCЃЌШчЭМЫљЪОЃЌвЊЧѓЛвЛИіШ§НЧаЮЃЌЪЙЫќгыІЄABCгавЛИіЙЋЙВЕФЖЅЕуCЃЌВЂЧвгыІЄABCШЋЕШЁЃ
МзЭЌбЇЕФЛЗЈШчЯТЃК
ЂйбгГЄBCКЭACЃЛ
ЂкдкBCЕФбгГЄЯпЩЯШЁЕуDЃЌЪЙCDЃНBCЃЛ
ЂлдкACЕФбгГЄЯпЩЯШЁЕуEЃЌЪЙCEЃНACЃЛ
ЂмСЌНгDEЃЌЕУІЄEDCЃЎ
ввЭЌбЇЕФЛЗЈШчЯТЃК
ЂйбгГЄACКЭBCЃЛ
ЂкдкBCЕФбгГЄЯпЩЯШЁЕуMЃЌЪЙCMЃНACЃЛ
ЂлдкACЕФбгГЄЯпЩЯШЁЕуNЃЌЪЙCNЃНBCЃЛ
ЂмСЌНгMNЃЌЕУІЄMNCЃЎ
ОПОЙФФжжЛЗЈЖд?гаШчЯТМИжжНсТлЃК
AЃЎМзЛЕУЖдЃЌввЛЕУВЛЖдЃЛ B. ввЛЕУЖдЃЌМзЛЕУВЛЖдЃЛ
CЃЎМзЁЂввЛЕУЖМЖдЃЛ DЃЎМзЁЂввЛЕУЖМВЛЖдЃЎ
е§ШЗЕФНсТлЪЧ .
етЕРЬтЛЙПЩвдАДЯТУцВНжшЭъГЩЃК
ЂйгУСПНЧЦїСПГіЁЯACBЕФЖШЪ§ЃЛ
ЂкдкЁЯACBЕФЭтВПЛЩфЯпCPЃЌЪЙЁЯACPЃНЁЯACBЃЛ
ЂлдкЩфЯпCPЩЯШЁЕуDЃЌЪЙCDЃНCBЃЛ
ЂмСЌНгADЃЎ
ІЄADCОЭЪЧЫљвЊЛЕФШ§НЧаЮЃЎ
етбљЛЕФНсЙћПЩМЧзїІЄABCЁе .
ТњзуЬтФПвЊЧѓЕФШ§НЧаЮПЩвдЛГіЖрЩйИіФи?
Д№АИЪЧ ЃЎЧыФудйЩшМЦвЛжжЛЗЈВЂЛГіЭМаЮЃЎ
ЁОД№АИЁПC;ІЄADC;ЮоЪ§Иі;ЭМаЮМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЁЂЃЈ2ЃЉРћгУЁАSASЁБПЩЖдМзЁЂввЕФЛЗЈНјааХаЖЯЃЛ
ЃЈ3ЃЉИљОнЁАSASЁБПЩХаЖЯ![]() Ёе
Ёе![]() ЃЛ
ЃЛ
ЃЈ4ЃЉвд![]() ЮЊЙЋЙВБпЛШ§НЧаЮгы
ЮЊЙЋЙВБпЛШ§НЧаЮгы![]() ШЋЕШЃЎ
ШЋЕШЃЎ
ЪдЬтНтЮіЃК(1)ЁЂ(2)ЖдгкМзЕФЛЗЈ,ПЩИљОнЁАSASЁБХаЖЈЁїACBЁеЁїECD;ЖдгкввЕФЛЗЈ,ПЩИљОнЁАSASЁБХаЖЈЁїACBЁеЁїMCNЃЌЫљвдМзЁЂввЖМЛЕУЖдЃЛ
(3)ИљОнЁАSASЁБПЩХаЖЯЁїABCЁеЁїADCЃЛ
(4)ТњзуЬтФПвЊЧѓЕФШ§НЧаЮПЩвдЛГіЮоЪ§ИіЃЛ
(5)ШчЭМ,Й§CЕузїCEЁЮABЃЌНиШЁCE=ABЃЌСЌНсBEЃЌдђЁїBCEЮЊЫљзї.
ЙЪД№АИЮЊЂлЃЌЁїADCЃЌЮоЪ§.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛзщЪ§ОнжаЕФУПвЛИіЪ§МѕШЅ40КѓЃЌЫљЕУаТЕФвЛзщЪ§ОнЕФЦНОљЪ§ЪЧ2ЃЌдђдРДФЧзщЪ§ОнЕФЦНОљЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 40 B. 42 C. 38 D. 2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћШ§НЧаЮЕФСНБпГЄЗжБ№ЮЊ3КЭ5ЃЌЕкШ§БпГЄЪЧХМЪ§ЃЌдђЕкШ§БпГЄПЩвдЪЧЃЈЁЁЁЁЃЉ
ЁЁЁЁAЃЎ2ЁЁЁЁBЃЎ3ЁЁЁЁCЃЎ4ЁЁЁЁDЃЎ8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЙ§ЕуCЕФжБЯпMNЁЮABЃЌDЮЊABБпЩЯвЛЕуЃЌЙ§ЕуDзїDEЁЭBCЃЌНЛжБЯпMNгкEЃЌДЙзуЮЊFЃЌСЌНгCDЃЌBEЃЎ 
ЃЈ1ЃЉЧѓжЄЃКCE=ADЃЛ
ЃЈ2ЃЉЕБDдкABжаЕуЪБЃЌХаЖЯЫФБпаЮBECDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєDЮЊABжаЕуЃЌдђЕБЁЯA=ЪБЃЌЫФБпаЮBECDЪЧе§ЗНаЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЯвADЪЧЁЯBACЕФЦНЗжЯпЃЌЙ§ЕуDзїЁбOЕФЧаЯпLЃЌЧвACЁЭDEЃЌДЙзуЮЊЕуE.

ЃЈ1ЃЉЧѓжЄЃКAD2=ABЁЄAE
ЃЈ2ЃЉШчЙћDE=![]() ЃЌCE=1ЃЌЧыХаБ№ЫФБпаЮACDOЕФаЮзДЃЌВЂжЄУїФуЕФНсТлГЩСЂ.
ЃЌCE=1ЃЌЧыХаБ№ЫФБпаЮACDOЕФаЮзДЃЌВЂжЄУїФуЕФНсТлГЩСЂ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЦНааЫФБпаЮABOCШчЭМЗХжУЃЌЕуAЁЂCЕФзјБъЗжБ№ЪЧЃЈ0ЃЌ4ЃЉЁЂЃЈЉ1ЃЌ0ЃЉЃЌНЋДЫЦНааЫФБпаЮШЦЕуOЫГЪБеыа§зЊ90ЁуЃЌЕУЕНЦНааЫФБпаЮAЁфBЁфOCЁфЃЎ
ЃЈ1ЃЉШєХзЮяЯпОЙ§ЕуCЁЂAЁЂAЁфЃЌЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуMЪБЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЮЪЃКЕБЕуMдкКЮДІЪБЃЌЁїAMAЁфЕФУцЛ§зюДѓЃПзюДѓУцЛ§ЪЧЖрЩйЃПВЂЧѓГіДЫЪБMЕФзјБъЃЛ
ЃЈ3ЃЉШєPЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌNЮЊxжсЩЯЕФвЛЖЏЕуЃЌЕуQзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌЕБPЁЂNЁЂBЁЂQЙЙГЩЦНааЫФБпаЮЪБЃЌЧѓЕуPЕФзјБъЃЌЕБетИіЦНааЫФБпаЮЮЊОиаЮЪБЃЌЧѓЕуNЕФзјБъЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуPЃЈЉ5ЃЌ3ЃЉдкЦНУцжБНЧзјБъЯЕжаЫљдкЕФЮЛжУЪЧЃЈЁЁЁЁЃЉ
A.ЕквЛЯѓЯоB.ЕкЖўЯѓЯоC.ЕкШ§ЯѓЯоD.ЕкЫФЯѓЯо
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com