
【题目】某商场计划购进A,B两种新型节能台灯共80盏,这两种台灯的进价、售价如下表所示:

(1)若商场的进货款为3700元,则这两种台灯各购进了多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的2倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
【答案】(1)应购进A型台灯30盏,B型台灯50盏;(2)购进27盏A型台灯,53盏B型台灯时,利润最大;最大利润为1865元.
【解析】
(1)设商场应购进A型台灯x盏,表示出B型台灯为(![]() )盏,然后根据进货款=A型台灯的进货款+B型台灯的进货款,列出方程求解即可;
)盏,然后根据进货款=A型台灯的进货款+B型台灯的进货款,列出方程求解即可;
(2)设商场销售完这批台灯可获利y元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
解:(1)设商场应购进A型台灯x盏,则B型台灯为(![]() )盏,
)盏,
根据题意得,40x+50(![]() )=3700,
)=3700,
解得:x=30,
∴![]() (盏);
(盏);
∴应购进A型台灯30盏,B型台灯50盏;
(2)设商场销售完这批台灯可获利y元,则
![]() ,
,
整理得:![]() ;
;
∵B型台灯的进货数量不超过A型台灯数量的2倍,
∴![]() ,
,
∴![]() ;
;
∵![]() ,y随x增大而减小,
,y随x增大而减小,
∴当![]() 时,利润y取最大值,
时,利润y取最大值,
即购进27盏A型台灯,53盏B型台灯时,利润最大;
∴最大利润为:![]() (元).
(元).


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
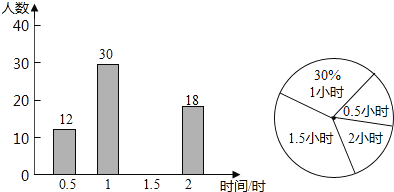
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把五张大小相同且分别写1、2、3、4、5的卡片放在一个暗箱中,先由甲随机从里面无放回地抽取两张,并记下两个数字之和后把卡片再放入暗箱,再由乙从里面无放回地抽取两张,并记下两个数字之和,若数字和为偶数则甲胜,若数字和为奇数则乙胜,则有( )
A.两者取胜的概率相同 B.甲胜的概率为0.6
C.乙胜的概率为0.6 D.乙胜的概率为0.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,过点
上一点,过点![]() 作
作![]() (垂足为
(垂足为![]() )交
)交![]() 于点
于点![]() ,且
,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() 交
交![]() 于点
于点![]()
![]() 求证:斜边
求证:斜边![]() 是
是![]() 的切线;
的切线;
![]() 设
设![]() 与
与![]() 相切的切点为
相切的切点为![]() ,
,![]() ,
,![]() ,连
,连![]() 、
、![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3).

(1)画△A'B'C',使△A'B'C'与△ABC关于y轴对称;
(2)在y轴上作一点P,使得PA+PC最短;
(3)将△ABC向右平移m个单位,向上平移n个单位,若点A落在第二象限内,且点C在第四象限内,则m的范围是 ,n的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
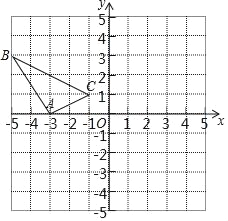
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:

(1)∠1=∠BAD;
(2)BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明设计两个可以自由转动的转盘,甲转盘被等分成![]() 个扇形,乙转盘被等分成
个扇形,乙转盘被等分成![]() 个扇形,每个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于
个扇形,每个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于![]() ,小颖获胜;指针所指区域内的数字之和等于
,小颖获胜;指针所指区域内的数字之和等于![]() ,为平局;指针所指区域内的数字之和大于
,为平局;指针所指区域内的数字之和大于![]() ,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
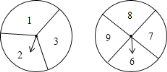
![]() 转动转盘甲,转盘停止后,指针指向偶数的概率是________.
转动转盘甲,转盘停止后,指针指向偶数的概率是________.
![]() 在此游戏中,小颖获胜的概率是________.
在此游戏中,小颖获胜的概率是________.
![]() 你认为该游戏是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,如果让你修改小明的方案,你认为应该从哪个方面入手(不用另外设计方案,只说明修改要点).
你认为该游戏是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,如果让你修改小明的方案,你认为应该从哪个方面入手(不用另外设计方案,只说明修改要点).
查看答案和解析>>
科目:初中数学 来源: 题型:
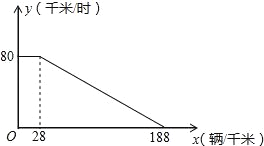
【题目】经研究表明,某市跨河大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,函数图象如图所示.
(1)求当28≤x≤188时,关于x的函数表达式;
(2)求车流量P(单位:辆/时)与车流密度x之间的函数关系式;(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
(3)若车流速度V不低于50千米时,求当车流密度x为多少时,车流量P达到最大,并求出这一最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com