
分析 (1)把m、n的值代入计算出m2+n2,m2-n2,2mn的值,再利用勾股定理逆定理进行证明即可;
(2)把m、n的值代入计算出m2+n2,m2-n2,2mn的值,再利用勾股定理逆定理进行证明即可;
(3)利用勾股定理逆定理验证两小边的平方和是否等于最长边的平方即可.
解答 解:(1)m=2,n=1时,
m2+n2=5,
m2-n2=3,
2mn=4,
∵32+42=52,
∴△ABC是直角三角形;
(2)当m=3,n=2时,
m2+n2=13,
m2-n2=5,
2mn=12,
∵52+122=132,
∴△ABC是直角三角形;
(3)∵(m2-n2)2+(2mn)2=m4+n4+2n2m2=(m2+n2)2,
∴对于m,n为任何正整数时(m>n),△ABC都为直角三角形.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| h(千米) | 0 | 1 | 2 | 3 | 4 | … |
| t(℃) | 24 | 18 | 12 | 6 | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
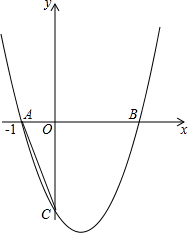 已知,如图,抛物线y=x2+bx+c的图象经过点A(-1,0),该抛物线与x轴的另一交点为B,与y轴的交点为C,tan∠CAO=3.
已知,如图,抛物线y=x2+bx+c的图象经过点A(-1,0),该抛物线与x轴的另一交点为B,与y轴的交点为C,tan∠CAO=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com