
【题目】如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E,连接DE交AB于点F.

求证:(1)CD=BE;
(2)AB垂直平分DE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等腰三角形三线合一的性质可得到AD⊥BC,再由角平分线的性质定理得到BE=BD,等量代换即可得到结论;
(2)根据HL证明Rt△AEB≌Rt△ADB,由全等三角形的性质可得到AE=AD,根据等腰三角形三线合一的性质,可得结论.
(1)∵AB=AC,点D是BC的中点,∴AD⊥BC.
又∵AE⊥BE,∴∠AEB=∠ADC=∠ADB=90°.
∵AB平分∠DAE,∴BE=BD.
∵BD=DC,∴CD=BE.
(2)在Rt△AEB和Rt△ADB中,∵BE=BD,AB=AB,∴Rt△AEB≌Rt△ADB(HL),∴AE=AD.
∵AB平分∠DAE,AE=AD,∴AB垂直平分DE.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过点O且平行于BC的直线交AB于点M,交AC于N,连接AO,则图中等腰三角形的个数为

A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
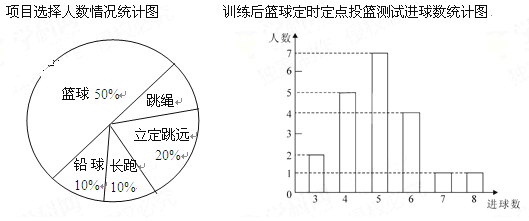
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(初步探索)
截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系;

(灵活运用)
(2)如图2,△ABC为等边三角形,直线a∥AB,D为BC边上一点,∠ADE交直线a于点E,且∠ADE=60°.求证:CD+CE=CA;

(延伸拓展)
(3)如图3,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若点E在CB的延长线上,点F在CD的延长线上,满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了了解七年级学生每周的课外阅读情况,通过问卷调查了该县七年级部分学生在某周的课外阅读量,把收集到的数据绘制成了如下的统计图,根据统计图中提供的信息,回答下列问题:

(1)参加问卷调查的有多少人?
(2)将阅读量在9﹣﹣12千字的直方图补充完整;
(3)求阅读量在6﹣﹣9千字内的扇形统计图中的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )

A.50°B.60°
C.45°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:![]() ,双曲线
,双曲线![]() ,在l上取一点
,在l上取一点![]() ,过
,过![]() 作x轴的垂线交双曲线于点
作x轴的垂线交双曲线于点![]() ,过
,过![]() 作y轴的垂线交l于点
作y轴的垂线交l于点![]() ,请继续操作并探究:过
,请继续操作并探究:过![]() 作x轴的垂线交双曲线于点
作x轴的垂线交双曲线于点![]() ,过
,过![]() 作y轴的垂线交l于点
作y轴的垂线交l于点![]() ,
,![]() ,这样依次得到l上的点
,这样依次得到l上的点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 记点
记点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,则
,则![]() ______;若要将上述操作无限次地进行下去,则
______;若要将上述操作无限次地进行下去,则![]() 不可能取的值是______.
不可能取的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过
经过![]() 的三个顶点,已知点
的三个顶点,已知点![]() ,
,![]() ,
,![]() 的直角顶点C在y轴上.
的直角顶点C在y轴上.
![]() 如图1,点D是抛物线
如图1,点D是抛物线![]() 第一象限内
第一象限内![]() 上的一个动点.
上的一个动点.
![]() 并直接写出点C的坐标,并求抛物线的解析式;
并直接写出点C的坐标,并求抛物线的解析式;
![]() 当动点D的坐标是多少时,四边形ABCD的面积最大?最大面积是多少?
当动点D的坐标是多少时,四边形ABCD的面积最大?最大面积是多少?
![]() 如图2,长度为1个单位长度的线段MN在
如图2,长度为1个单位长度的线段MN在![]() 的边AB上运动,过M,N分别作AB的垂线交直角边于P,Q两点.
的边AB上运动,过M,N分别作AB的垂线交直角边于P,Q两点.
![]() 在线段MN运动过程中,若四边形MNQP是矩形,求点M的坐标;
在线段MN运动过程中,若四边形MNQP是矩形,求点M的坐标;
![]() 在线段MN运动过程中,若以C、P、Q为顶点的三角形与
在线段MN运动过程中,若以C、P、Q为顶点的三角形与![]() 相似,直接写出点M的坐标.
相似,直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com