
【题目】列一元一次方程解应用题:
2019年6月以来猪肉价格不断走高,引起了民众与政府的高度关注,市场猪肉的单价涨到每千克50元时,政府决定投入储备猪肉以平抑猪肉价格.2019年12月,政对投放储备猪肉4万吨,投放后民众开始大量采购,某超市也做了相应的促销活动如下:
一次性购买数量(千克) | 返还金额 |
不超过20千克 | 一律按售价返还 |
超过20千克,但不超过40千克 | 一律按售价返还 |
超过40千克 | 除按售价返还 |
例如:某顾客买了45千克猪肉,则实际付款为:![]() (元).
(元).
(1)该超市在促销前购进了一批猪肉,促销前以每千克50元的单价卖出10千克,促销期间以同样的单价卖了30千克给小明家.结果发现,促销前卖出的10千克猪肉获得的利润跟卖给小明家的30千克猪肉获得的利润一样多,求该超市购进这批猪肉的进价为每千克多少元?
(2)促销期间,小红家从该超市以每千克50元的单价分两次共购买猪肉80千克,第一次购买的数量少于第二次购买的数量,若两次实际共付款2990元,则小红家两次分别购买猪肉多少千克?
【答案】(1)35;(2)两次分别购买猪肉8千克、72千克.
【解析】
(1)设该超市购进这批猪肉的进价为每千克x元,根据“促销前卖出的10千克猪肉获得的利润跟卖给小明家的30千克猪肉获得的利润一样多”,列方程求出结果;
(2)设促销期间小红家第一次购买猪肉x千克,根据两次实际共付款2990元,即可得出关于y的一元一次方程,解之即可得出结论,注意要分类讨论.
解:(1)设该超市购进这批猪肉的进价为每千克x元,
依题意,得:![]() ,
,
解得:x=35.
答:该超市购进这批猪肉的进价为每千克35元;
(2)设促销期间小红家第一次购买猪肉x千克,因为第一次购买的数量少于第二次购买的数量,所以分以下两种情况:
①![]() 时,80-x>40,
时,80-x>40,
依题意,得: ![]() ,
,
解得:x=8,
80-x=72;
②![]() 时,80-x>40,
时,80-x>40,
依题意,得:![]() ,
,
解得:x=16,
16<20,舍去,
答:小红家两次分别购买猪肉8千克、72千克.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的某圆上,有弦MN,取MN的中点P,我们规定:点P到某点(直线)的距离叫做“弦中距”,用符号“![]() ”表示.
”表示.
现请在以W(-3,0)为圆心,半径为2的⊙W圆上,根据以下条件解答所提问题:
(1)已知弦MN长度为2.
①如图1:当MN∥x轴时,直接写出到原点O的![]() 的长度;
的长度;
②如果MN在圆上运动时,在图2中画出示意图,并直接写出到点O的![]() 的取值范围.
的取值范围.
(2)已知点![]() ,点N为⊙W上的一动点,有直线
,点N为⊙W上的一动点,有直线![]() ,求到直线
,求到直线![]() 的
的![]() 的最大值.
的最大值.
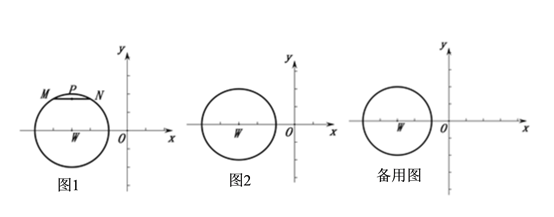
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级二班的几位同学正在一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点![]() 、
、![]() 表示的数都是绝对值是4的数”;
表示的数都是绝对值是4的数”;
乙说:“点![]() 表示负整数,点
表示负整数,点![]() 表示正整数,且这两个数的差是3”;
表示正整数,且这两个数的差是3”;
丙说:“点![]() 表示的数的相反数是它本身”.
表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,画出一条数轴,并描出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个不同的点.
五个不同的点.
(2)求这个五个点表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某小学“演讲大赛”选拔赛初赛中,甲、乙、丙三位评委对小选手的综合表现,分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论.
⑴请用树状图表示出三位评委给小选手琪琪的所有可能的结论;
⑵对于小选手琪琪,只有甲、乙两位评委给出相同结论的概率是多少?
⑶比赛规定,三位评委中至少有两位给出“通过”的结论,则小选手可入围进入复赛,问琪琪进入复赛的概率是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
材料一:
自然数的发现是人类数学研究的开端,我们在研究自然数的时候采用的进制为十进制.现定义:位数相同且对应数位上的数字之和为10的两个数互为“亲密数”,例如:3与7互为“亲密数”,16的“亲密数”为94.
材料二:
若![]() 的“亲密数”为
的“亲密数”为![]() ,记
,记![]() 为
为![]() 的“亲密差”例如:72的“亲密数”为38.
的“亲密差”例如:72的“亲密数”为38.
![]() ,则34为72的“亲密差”.
,则34为72的“亲密差”.
根据材料,回答下列问题:
(1)请填空:64的“亲密数”为______;25的“亲密差”为______;
(2)某两位数个位上的数字比十位上的数字大2,且这个两位数的“亲密数”等于它的![]() 倍,求这个两位数的“亲密差”:
倍,求这个两位数的“亲密差”:
(3)某个三位数![]() (
(![]() ,且
,且![]() 为整数),记
为整数),记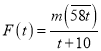 ,若
,若![]() 的值为一个整数,求这个整数
的值为一个整数,求这个整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
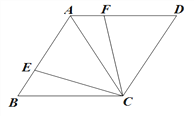
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
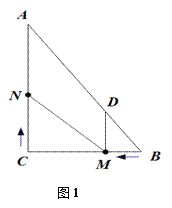
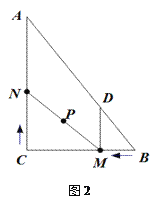
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
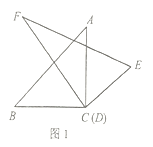
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
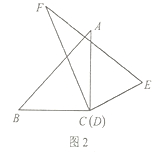
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
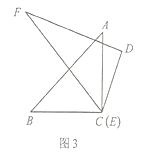
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com