
分析 (1)根据零指数幂和负整数指数幂的意义得到原式=$\frac{1}{4}$+1+1.25-1+$\frac{1}{2}$,然后进行加减运算即可;
(2)先利用平方差公式计算,然后合并即可.
解答 解:(1)原式=$\frac{1}{4}$+1+1.25-1+$\frac{1}{2}$
=2;
(2)原式=(3-2)×$\sqrt{2}$+$\frac{\sqrt{2}}{4}$
=$\sqrt{2}$+$\frac{\sqrt{2}}{4}$
=$\frac{5\sqrt{2}}{4}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.


科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 每辆汽车能装载的质量/吨 | 1 | 1.5 |
| 每吨蔬菜可获利润/百元 | 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
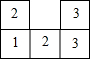 一个几何体由大小相同的立方块搭成,从上面看到的如图所示,其中小正方形中的数字表示在该位置的立方块个数.若允许从该几何体中拿掉部分立方块,使剩下的几何体从正面和上面看的形状相同,则拿掉的立方块数量最多是( )
一个几何体由大小相同的立方块搭成,从上面看到的如图所示,其中小正方形中的数字表示在该位置的立方块个数.若允许从该几何体中拿掉部分立方块,使剩下的几何体从正面和上面看的形状相同,则拿掉的立方块数量最多是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
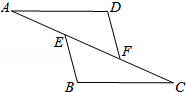 如图,已知点E,F在AC上,AD∥BC,DF=BE,添加的一个条件(不要在图中增加任何字母和线),使△ADF≌△CBE.你添加的条件是:∠D=∠B.
如图,已知点E,F在AC上,AD∥BC,DF=BE,添加的一个条件(不要在图中增加任何字母和线),使△ADF≌△CBE.你添加的条件是:∠D=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com