
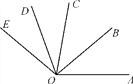
【题目】如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
【答案】40°.
【解析】试题分析:(1)根据角平分线的定义可以求得∠BOD=∠AOB+∠DOE;
(2)根据角平分线的定义易求得∠EOC=2∠COD=60°,所以由图中的角与角间的和差关系可以求得∠AOC=80°,最后由角平分线的定义求解.
试题解析:解:(1)因为OB为∠AOC的平分线,OD是∠COE的平分线,
所以∠AOB=∠BOC,∠DOE=∠DOC.
所以∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°.
(2)因为OD是∠COE的平分线,∠COD=30°,
所以∠EOC=2∠COD=60°.
因为∠AOE=140°,∠AOC=∠AOE-∠EOC=80°.
又因为OB为∠AOC的平分线,
所以∠AOB=![]() ∠AOC=40°.
∠AOC=40°.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示.
时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(1)你认为哪位学生抽取的样本不合理?请说明理由.
(2)专家建议每周上网2小时以上(含2小时)的学生应适当减少上网的时间,估计该校全体初二学生中有多少名学生应适当减少上网的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
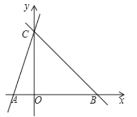
【题目】如图,直线y=kx+k交x轴,y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45.
(1)求直线BC的解析式;
(2)动点P从A出发沿射线AB匀速运动,速度为2个单位/秒,连接CP,设△PBC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,直接写出t的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果店主分两批购进某一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果的单价是多少元?
(2)该水果店主计两批水果的售价均定为每箱40元,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了20%的损耗,但这两批水果销售完后仍赚了不低于1716元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
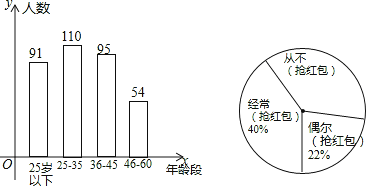
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是直线
是直线![]() 上的一点,将一直角三角板如图摆放,过点
上的一点,将一直角三角板如图摆放,过点![]() 作射线
作射线![]() 平分
平分![]() .当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现
.当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
(1)如图1,当![]() 时,若
时,若![]() ,求
,求![]() 的度数;
的度数;
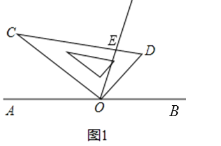
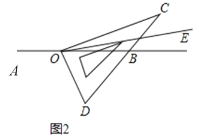
(2)如图2,当![]() 是钝角时,使得直角边
是钝角时,使得直角边![]() 在直线
在直线![]() 的上方,若
的上方,若![]() ,其他条件不变,直接写出
,其他条件不变,直接写出![]() 的度数;
的度数;
(3)若![]() ,在旋转过程中你发现
,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?请你直接用含
之间有怎样的数量关系?请你直接用含![]() 的代数式表示
的代数式表示![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市决定购进甲、乙两种取暖器,已知甲种取暖器每台进价比乙种取暖器多500元, 用40000元购进甲种取暖器的数量与用30000元购进乙种取暖器的数量相同.请解答下列问题:
(1)求甲、乙两种取暖器每台的进价;
(2)若甲种取暖器每台售价2500元,乙种取暖器每台售价1800元,超市欲同时购进两种取暖器20 台,且全部售出.设购进甲种取暖器x(台),所获利润为y(元),试用关于x的式子表示y;
(3)在(2)的条件下,若超市计划用不超过36000元购进取暖器,且甲种取暖器至少购进10台, 并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器. 求购买按摩器的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
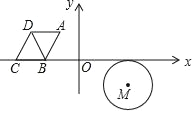
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com