
【题目】如图,点![]() 是直线
是直线![]() 上的一点,将一直角三角板如图摆放,过点
上的一点,将一直角三角板如图摆放,过点![]() 作射线
作射线![]() 平分
平分![]() .当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现
.当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
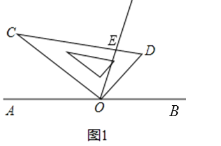
(1)如图1,当![]() 时,若
时,若![]() ,求
,求![]() 的度数;
的度数;
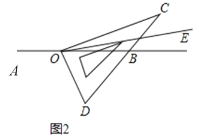
(2)如图2,当![]() 是钝角时,使得直角边
是钝角时,使得直角边![]() 在直线
在直线![]() 的上方,若
的上方,若![]() ,其他条件不变,直接写出
,其他条件不变,直接写出![]() 的度数;
的度数;
(3)若![]() ,在旋转过程中你发现
,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?请你直接用含
之间有怎样的数量关系?请你直接用含![]() 的代数式表示
的代数式表示![]() 的度数;
的度数;
【答案】(1)20°;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据角平分线的作法作出OE平分∠BOC,先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(2)先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(3)分两种情况:0°≤∠AOC≤180°,0°≤∠DOE≤180°,可求∠AOC与∠DOE之间的数量关系.
解:(1)∵∠AOC+∠BOC=180°,∠AOC=40°,
∴∠BOC=140°,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC 70°,
∠BOC 70°,
∵∠COD=90°,
∴∠DOE=∠COD-∠COE=20°;
(2)∵∠AOC+∠BOC=180°,∠AOC=160°,
∴∠BOC=180°-160°=20°;
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=10°,
∠BOC=10°,
∵∠COD=90°,
∴∠DOE=90°-10°=80°;
(3)当OC在AB上方时,∠DOE的度数为![]() ,
,
∵∠AOC=α,
∴∠BOC=180°-α,
∵OE平分∠BOC,
∴∠COE=90°-![]() ,
,
∴∠DOE=90°-(90°-![]() )=
)=![]() ,
,
同理:当OC在AB下方时,∠DOE=180°-![]() .
.
∴∠DOE=![]() ∠AOC=
∠AOC=![]() (0°≤∠AOC≤180°),
(0°≤∠AOC≤180°),
∠DOE=180°-![]() ∠AOC=180°-
∠AOC=180°-![]() (0°≤∠DOE≤180°).
(0°≤∠DOE≤180°).


科目:初中数学 来源: 题型:
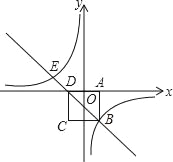
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数![]() 的图象交于点B、E.
的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求完成下列题目
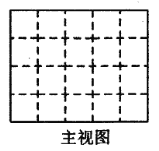
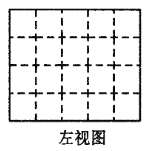
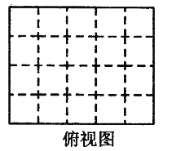
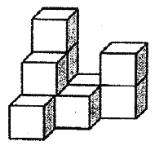
(1)图中有______块小正方体;
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和主视图与你在上图方格中所画的图一致,若这样的几何体最少要个![]() 小正方体,最多要
小正方体,最多要![]() 个小正方体,则
个小正方体,则![]() 的值为___________.
的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
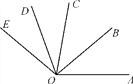
【题目】如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元,厂方开展促销活动期间,向客户提供两种优惠方法:①买一套西装送一条领带;②西装和领带均按定价的90%付款。某商店到该服装厂购买西装20件,领带若干条.
(1)领带买多少条时,两种优惠方法相同?
(2)购买50条领带时,应采用哪一种方案更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
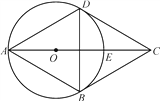
【题目】已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
(1)判断⊙O与BC的位置关系,并说明理由;
(2)若CE=2,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
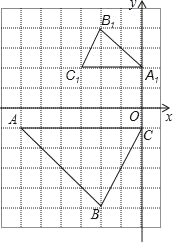
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
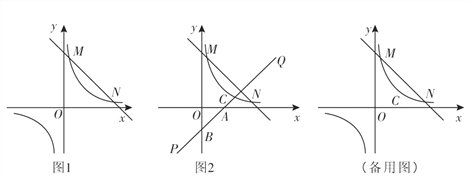
【题目】如图1 ,一次函数![]() (k,b为常数,k≠0)的图象与反比例函数
(k,b为常数,k≠0)的图象与反比例函数![]() (m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(1)填空:①反比例函数的解析式是 ; ②根据图象写出![]() 时自变量x的取值范围是 ;
时自变量x的取值范围是 ;
(2) 若将直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,求a的值;
(3) 如图2,函数![]() 的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交
的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交![]() 轴于点A,交
轴于点A,交![]() 轴点B,若BC=2CA, 求OA·OB的值.
轴点B,若BC=2CA, 求OA·OB的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com