
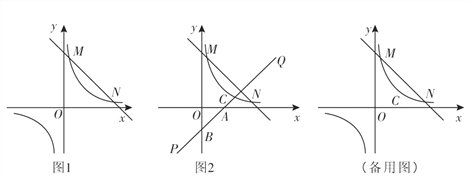
【题目】如图1 ,一次函数![]() (k,b为常数,k≠0)的图象与反比例函数
(k,b为常数,k≠0)的图象与反比例函数![]() (m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(1)填空:①反比例函数的解析式是 ; ②根据图象写出![]() 时自变量x的取值范围是 ;
时自变量x的取值范围是 ;
(2) 若将直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,求a的值;
(3) 如图2,函数![]() 的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交
的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交![]() 轴于点A,交
轴于点A,交![]() 轴点B,若BC=2CA, 求OA·OB的值.
轴点B,若BC=2CA, 求OA·OB的值.
![]()
【答案】(1) ① y=![]() .②
.②![]() ;(2) a=1或a=9.;(3) 18或2..
;(2) a=1或a=9.;(3) 18或2..
【解析】整体分析:
(1)由点A的坐标求反比例函数的解析式,得到点B的坐标; ![]() ,即是一次函数的图象在反比例函数图象的下方时自变量的范围;(2)由点M,N的坐标求直线MN的解析式,直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,即是方程kx+b-a=
,即是一次函数的图象在反比例函数图象的下方时自变量的范围;(2)由点M,N的坐标求直线MN的解析式,直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,即是方程kx+b-a=![]() 的判别式等于0;(3)设点C(a,b),根据BC=2CA,分三种情况讨论,利用△ACH∽△ABO,结合ab=4求解.
的判别式等于0;(3)设点C(a,b),根据BC=2CA,分三种情况讨论,利用△ACH∽△ABO,结合ab=4求解.
解:(1)k=1×4=4,所以y=![]() .
.
②当y=4时,x=![]() ,则B(4,1).
,则B(4,1).
根据图象得: ![]() .
.
(2)点M(1,4)和点N(4,1)分别代入![]() 得
得![]()
直线AB向下平移a个单位长度后的解析式为y=-x+5-a,
把y=![]() 代入消去y,整理,得x2-(5-a)x+4=0.
代入消去y,整理,得x2-(5-a)x+4=0.
∵平移后的直线与反比例函数的图象有且只有一个公共点,
∴Δ=(5-a)2-16=0.
解得a=1或a=9.
(3)设点C(a,b),则ab=4如图1,过C点作CH⊥OA于点H.
①当点B在y轴的负半轴时,如图1
∵BC=2CA,∴AB=CA.
∵∠AOB=∠AHC=90°,∠1=∠2,
∴△ACH∽△ABO.
∴OB=CH=b,OA=AH=0.5a
∴![]() .
.
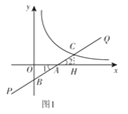
②当点B在y轴的正半轴时,
如图2,当点A在x轴的正半轴时,
∵BC=2CA,∴. ![]()
∵CH∥OB,∴△ACH∽△ABO.
∴![]()
∴.OB=3b,OA=1.5a
∴![]() .
.
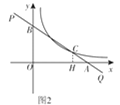
如图3,当点A在x轴的负半轴时,BC=2CA不可能.
综上所述,OA·OB的值为18或2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 是直线
是直线![]() 上的一点,将一直角三角板如图摆放,过点
上的一点,将一直角三角板如图摆放,过点![]() 作射线
作射线![]() 平分
平分![]() .当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现
.当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
(1)如图1,当![]() 时,若
时,若![]() ,求
,求![]() 的度数;
的度数;
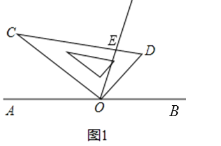
(2)如图2,当![]() 是钝角时,使得直角边
是钝角时,使得直角边![]() 在直线
在直线![]() 的上方,若
的上方,若![]() ,其他条件不变,直接写出
,其他条件不变,直接写出![]() 的度数;
的度数;
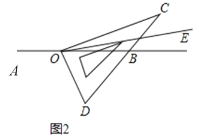
(3)若![]() ,在旋转过程中你发现
,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?请你直接用含
之间有怎样的数量关系?请你直接用含![]() 的代数式表示
的代数式表示![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据: ![]() ,
, ![]() )
)
(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

查看答案和解析>>
科目:初中数学 来源: 题型:
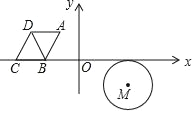
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
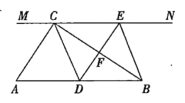
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当![]() 为
为![]() 的中点时,四边形
的中点时,四边形![]() 是什么特殊四边形?请说明你的理由;
是什么特殊四边形?请说明你的理由;
(3)若![]() 为
为![]() 的中点,则当
的中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量 | 单价 |
不超过12 m3的部分 | a元∕m3 |
超过12 m3但不超过20 m3的部分 | 1.5a元∕m3 |
超过20 m3的部分 | 2a元∕m3 |
(1) 当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2) 设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费_____________元(用含a、n的整式表示);
(3) 当a=2时,甲、乙两用户一个月共用水40 m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.

(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B.求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米.
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:①CB=CE;②D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
![]()
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com