
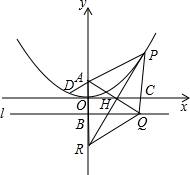
 如图,在直角坐标系xOy中,点P为函数y=$\frac{1}{4}$x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R,连结PA并延长交函数y=$\frac{1}{4}$x2的图象于D.
如图,在直角坐标系xOy中,点P为函数y=$\frac{1}{4}$x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R,连结PA并延长交函数y=$\frac{1}{4}$x2的图象于D.分析 (1)由A(0,1),B(0,-1)得到OA=OB,再由BQ∥x轴得到OH为△AOQ的中位线,所以AH=QH;
(2)①先利用PQ∥AB得到∠RAH=∠PQH,再根据“ASA”证明△AHR≌△QHP,则AR=PQ,而AR∥PQ,于是可判断四边形APQR为平行四边形;
②根据二次函数图象上点的坐标特征设P(m,$\frac{1}{4}$m2),则PQ=$\frac{1}{4}$m2+1,再利用两点间的距离公式计算出PA=$\frac{1}{4}$m2+1,则PA=PQ,于是根据菱形的判定方法得到平行四边形APQR为菱形;
(3)先表示出H($\frac{m}{2}$,0),再利用待定系数法求出直线PH的解析式为y=$\frac{m}{2}$x-$\frac{1}{4}$m2,接着通过解方程组$\left\{\begin{array}{l}{y=\frac{m}{2}x-\frac{1}{4}{m}^{2}}\\{y=\frac{1}{4}{m}^{2}}\end{array}\right.$得直线PH与抛物线y=$\frac{1}{4}$x2的交点坐标为(m,$\frac{1}{4}$m2),此点P点,由此可判断除P点外,直线PH与抛物线y=$\frac{1}{4}$x2没有其它公共点;
(4)作EF∥y轴交PD于F点,如图,通过解方程组$\left\{\begin{array}{l}{y=2x+1}\\{y=\frac{1}{4}{x}^{2}}\end{array}\right.$得D(4-2$\sqrt{5}$,9-4$\sqrt{5}$),P(4+2$\sqrt{5}$,9+4$\sqrt{5}$),
设E(t,$\frac{1}{4}$t2),则F(t,2t+1),EF=2t+1-$\frac{1}{4}$t2,则可根据三角形面积公式计算出S△PDE=S△PEF+S△DEF=-$\frac{\sqrt{5}}{2}$t2+4$\sqrt{5}$t+2$\sqrt{5}$,然后根据二次函数的性质求出S△PDE最大时t的值,则可得到此时E点坐标.
解答 (1)证明:∵A(0,1),B(0,-1),
∴OA=OB,
∵BQ∥x轴,
∴OH为△AOQ的中位线,
∴AH=QH,即H点为线段AQ的中点;
(2)证明:①∵PQ∥AB,
∴∠RAH=∠PQH,
在△AHR和△QHP中,
$\left\{\begin{array}{l}{∠RAH=∠PQH}\\{AH=QH}\\{∠AHR=∠PHQ}\end{array}\right.$,
∴△AHR≌△QHP,
∴AR=PQ,
而AR∥PQ,
∴四边形APQR为平行四边形;
②设P(m,$\frac{1}{4}$m2),
∵PQ∥y轴,
∴Q(m,-1),
∴PQ=$\frac{1}{4}$m2+1,
∵PA=$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$=$\sqrt{(\frac{1}{4}{m}^{2}+1)^{2}}$=$\frac{1}{4}$m2+1,
∴PA=PQ,
∴平行四边形APQR为菱形;
(3)解:除P点外,直线PH与抛物线y=$\frac{1}{4}$x2没有其它公共点.理由如下:
∵A(0,1),Q(m,-1),
而H点为AQ的中点,
∴H($\frac{m}{2}$,0),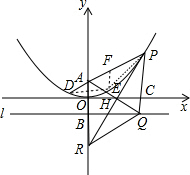 设直线PH的解析式为y=kx+b,
设直线PH的解析式为y=kx+b,
把H($\frac{m}{2}$,0),P(m,$\frac{1}{4}$m2)代入得$\left\{\begin{array}{l}{\frac{m}{2}k+b=0}\\{mk+b=\frac{1}{4}{m}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{m}{2}}\\{b=-\frac{1}{4}{m}^{2}}\end{array}\right.$,
∴直线PH的解析式为y=$\frac{m}{2}$x-$\frac{1}{4}$m2,
解方程组$\left\{\begin{array}{l}{y=\frac{m}{2}x-\frac{1}{4}{m}^{2}}\\{y=\frac{1}{4}{m}^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=m}\\{y=\frac{1}{4}{m}^{2}}\end{array}\right.$,即直线PH与抛物线y=$\frac{1}{4}$x2的交点坐标为(m,$\frac{1}{4}$m2),
∴除P点外,直线PH与抛物线y=$\frac{1}{4}$x2没有其它公共点;
(4)解:作EF∥y轴交PD于F点,如图,
解方程组$\left\{\begin{array}{l}{y=2x+1}\\{y=\frac{1}{4}{x}^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=4-2\sqrt{5}}\\{y=9-4\sqrt{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=4+2\sqrt{5}}\\{y=9+4\sqrt{5}}\end{array}\right.$,则D(4-2$\sqrt{5}$,9-4$\sqrt{5}$),P(4+2$\sqrt{5}$,9+4$\sqrt{5}$),
设E(t,$\frac{1}{4}$t2),则F(t,2t+1),
∴EF=2t+1-$\frac{1}{4}$t2,
∴S△PDE=S△PEF+S△DEF
=$\frac{1}{2}$•(2$\sqrt{5}$+2$\sqrt{5}$)•(2t+1-$\frac{1}{4}$t2)
=-$\frac{\sqrt{5}}{2}$t2+4$\sqrt{5}$t+2$\sqrt{5}$,
当t=-$\frac{4\sqrt{5}}{2×(-\frac{\sqrt{5}}{2})}$=4时,S△PDE最大,
此时E点坐标为(4,4).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形与菱形的判定方法;会利用待定系数法求一次函数与二次函数的解析式;理解坐标与图形性质.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:填空题
 拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是y=-$\frac{1}{8}$x2.
拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是y=-$\frac{1}{8}$x2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
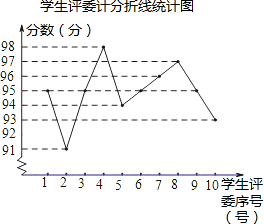
| 评委序号/号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 计分/分 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
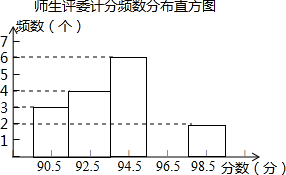
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
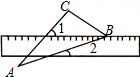 将一把有刻度的直尺摆放在含30°角的三角板(∠A=30°,∠C=90°)上,其中顶点B在直尺的一边上,已知∠1=55°,则∠2=25度.
将一把有刻度的直尺摆放在含30°角的三角板(∠A=30°,∠C=90°)上,其中顶点B在直尺的一边上,已知∠1=55°,则∠2=25度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
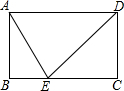 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com