
分析 (1)根据中位数、众数的定义,可得答案;
(2)根据圆周角360°乘以A类所占的比例,可得答案;
(3)根据折线统计图、扇形统计图,可获得有效信息.
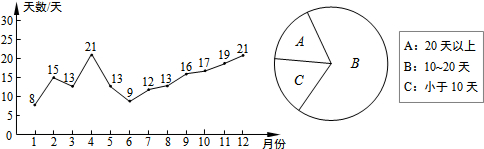
解答 解:(1)由小到大的顺序排列数据8,9,12,13,13,13,15,16,17,19,21,21,
中位数是$\frac{13+15}{2}$=14,众数是13,
故答案为:14,13;
(2)扇形统计图中扇形A的圆心角的度数360°×$\frac{2}{12}$=60°;
(3)该市2014年每月空气质量达到良好以上天数的平均数是14$\frac{3}{4}$,中位数是14,众数是13,空气质量达到良好的天数较少;该市下半年的空气质量呈逐渐向好趋势;该市4,12月空气质量较好,2,3,5,7,8,9,10,11月一般,1,6月较差.
点评 本题考查了折线统计图,在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比;求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 人数 | 甲旅行社 | 乙旅行社 |
| 少于250人 | 一律八折优惠 | 七折优惠 |
| 不少于250人 | 五折优惠 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=2AD,AP平分∠DAB,且AP⊥DP于点P,连接CP,则sin∠DCP的值是$\frac{\sqrt{10}}{10}$.
如图,矩形ABCD中,AB=2AD,AP平分∠DAB,且AP⊥DP于点P,连接CP,则sin∠DCP的值是$\frac{\sqrt{10}}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
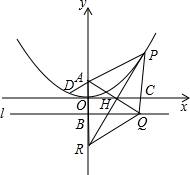 如图,在直角坐标系xOy中,点P为函数y=$\frac{1}{4}$x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R,连结PA并延长交函数y=$\frac{1}{4}$x2的图象于D.
如图,在直角坐标系xOy中,点P为函数y=$\frac{1}{4}$x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R,连结PA并延长交函数y=$\frac{1}{4}$x2的图象于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 众数 | C. | 中位数 | D. | 平均数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com