
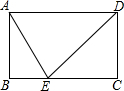
 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 12 |
分析 由矩形的性质求得AB=CD,AD=BC,∠B=∠C=90°,AD∥BC,进而根据平行线的性质得出cos∠AEB=$\frac{1}{2}$,tan∠DEC=1,设BE=x,根据cos∠AEB=$\frac{BE}{AE}$=$\frac{x}{AE}$=$\frac{1}{2}$,得出AE=2x,然后根据勾股定理求得AB=$\sqrt{3}$x,根据面积求得x的值,从而求得DC的长,由tan∠DEC=1,得出DC=EC=2$\sqrt{3}$,根据三角形面积公式求得即可.
解答 解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠B=∠C=90°,AD∥BC,
∴∠AEB=∠DAE,∠DEC=∠ADE,
∵cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,
∴cos∠AEB=$\frac{1}{2}$,tan∠DEC=1,
设BE=x,
在RT△ABE中,cos∠AEB=$\frac{BE}{AE}$=$\frac{x}{AE}$=$\frac{1}{2}$,
∴AE=2x,
∴AB=$\sqrt{A{E}^{2}-B{E}^{2}}$=$\sqrt{3}$x
∵△ABE的面积是2$\sqrt{3}$,
∴$\frac{1}{2}$x•$\sqrt{3}$x=2$\sqrt{3}$,解得x=2,
∴AB=$\sqrt{3}$x=2$\sqrt{3}$,
∴DC=AB=2$\sqrt{3}$,
在RT△ECD中,tan∠DEC=1,
∴$\frac{DC}{EC}$=1,
∴DC=EC=2$\sqrt{3}$,
∴S△ECD=$\frac{1}{2}$DC•EC=$\frac{1}{2}$×$2\sqrt{3}$×$2\sqrt{3}$=6.
故选C.
点评 本题考查了矩形的性质、勾股定理和直角三角函数等,根据三角形的面积、三角函数、勾股定理求得AB的长是解题的关键.


科目:初中数学 来源: 题型:解答题
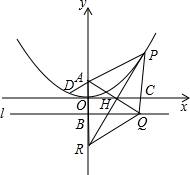 如图,在直角坐标系xOy中,点P为函数y=$\frac{1}{4}$x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R,连结PA并延长交函数y=$\frac{1}{4}$x2的图象于D.
如图,在直角坐标系xOy中,点P为函数y=$\frac{1}{4}$x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R,连结PA并延长交函数y=$\frac{1}{4}$x2的图象于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 众数 | C. | 中位数 | D. | 平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
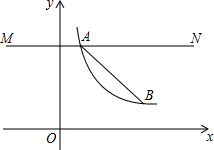 如图,点A、B是反比例函数第一象限图象上的两点,且坐标分别为(1,n),(n,$\frac{n}{4}$),直线MN过点A且与x轴平行.
如图,点A、B是反比例函数第一象限图象上的两点,且坐标分别为(1,n),(n,$\frac{n}{4}$),直线MN过点A且与x轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
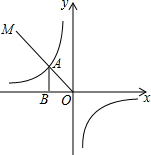 如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.
如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
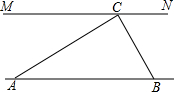 为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com