
����Ŀ����֪����ͼA��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��10��B���Ӧ����Ϊ70 ![]()
��1����д��AB���е�M��Ӧ����
��2��������һֻ��������P��A���������3����λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�B���������2����λ/����ٶ������˶�������ֻ���������������ϵ�C���������������C���Ӧ����
��3��������������P��A���������3����λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�B���������2��λ/����ٶ������˶��������ʱ����ֻ�������������������35����λ���ȣ���д����ʱP���Ӧ������
���𰸡�
��1���⣺M���Ӧ�����ǣ���10+70����2=30
��2���⣺��A��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��10��B���Ӧ����Ϊ70��
��AB=70+10=80��
��t���P��Q������
��3t+2t=80�����t=16��
���ʱ��Q�߹���·��=3��16=48��
���ʱC���ʾ����Ϊ��10+48=38��
��C���Ӧ������38
��3���⣺����ǰ����80��35���£�2+3��=9���룩��
������35+80���£�2+3��=23���룩��
��9���23�룬2ֻ�������������������35����λ���ȣ�9���Ӧ����Ϊ17��23���Ӧ����Ϊ59
����������1����10��70�͵�һ�뼴��M��Ӧ��������2�������AB�ij�������t���P��Q�������ɵó�����t��һԪһ�η��̣����t��ֵ�������P��Q����ʱ��Q�ƶ��ľ��룬�����ɵó�C���Ӧ��������3����Ϊ2ֻ������������ǰ���35����λ���Ⱥ����������35����λ���ȣ�����ǰ����80��35���£�2+3��=9���룩��������35+80���£�2+3��=23���룩��
�����㾫����������Ĺؼ�����������������֪ʶ�����������ǹ涨��ԭ�㡢������λ���ȵ�һ��ֱ�ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����BD����ABC��һ����ƽ���ߣ���O��E��F�ֱ���BD��BC��AC�ϣ����ı���OECF�������Σ�

��1����֤����O����BAC��ƽ�����ϣ�
��2����AC=5��BC=12����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=2x-a��x��Ľ����ǵ㣨-2��0������y��ĶԳƵ㣬��һԪһ�β���ʽ2x-a��0�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx������A����3��4����ֱ��l��x���ཻ�ڵ�B������AOB��ƽ�����ཻ�ڵ�C��ֱ��l�Ľ���ʽΪy=kx��5k��k��0����BC=OB��
��1������C�ڴ��������ϣ��������ߵĽ���ʽ��
��2���ڣ�1���������£�����A��y���ƽ���ߣ���ֱ��l�ཻ�ڵ�D����PΪ�������ϵ�һ�����㣬����PA��PD����![]() ʱ�����P�����꣮
ʱ�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
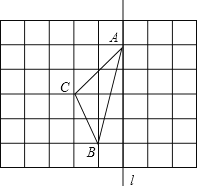
����Ŀ����ͼ���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���A��B��C��С�����εĶ����ϣ�
��1����ͼ�л��������ֱ��![]() ����ԳƵġ�A��B��C����
����ԳƵġ�A��B��C����
��2���߶�CC�䱻ֱ��![]() ��������������
��������������
��3����ABC�������������������
��4����ֱ��![]() ����һ��P��ʹPB+PC�ij���̣�
����һ��P��ʹPB+PC�ij���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
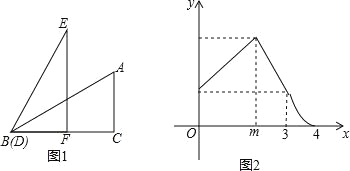
����Ŀ����ͼ1������ȫ�ȵ���ABC����DEF�У���ACB=��DFE=90�㣬AB=DE�����е�B�͵�D�غϣ���F��BC�ϣ�����DEF������BCƽ�ƣ���ƽ�Ƶľ���Ϊx��ƽ�ƺ��ͼ������ABC�غϲ��ֵ����Ϊy��y����x�ĺ���ͼ����ͼ2��ʾ������0��x��m��m��x��3��3��x��4ʱ�������Ľ���ʽ��ͬ��
��1����գ�BC�ij�Ϊ ��
��2����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������4�ſ�Ƭд�Ų�ͬ�����ֵĿ�Ƭ�����㰴Ҫ������Ƭ��������и����⣺ ![]()
��1������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֳ˻������γ�ȡ�����ֵ�Ƕ��٣�
��2������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������һ������������γ�ȡ���������Ƕ��٣�
��3������4�ſ�Ƭ�ϵ�������ѧ�������㷽����ʹ���Ϊ24��д������ʽ�ӣ�һ�ּ��ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����D��ֱ��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE=��BAC������CE��
��1����ͼ1������D���߶�BC�ϣ������BAC=90�������BCE=�����ȣ�
��2�����BAC=������BCE=�£�
����ͼ2������D���߶�BC���ƶ�����������֮����������������ϵ����˵�����ɣ�
�ڵ���D��ֱ��BC���ƶ�����������֮����������������ϵ����ֱ��д����Ľ��ۣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com